从定义域到值域

定义域：原始值的集合，比如几个学生的姓名{小明，小王，小张}

值域：目标值的集合，比如几个学生的学号{1,2,3}

映射：(原始值,目标值)对的集合，反映从定义域的某个值变成某个值的对应关系，比如学生和学号的对应关系{(1,小明)，(2,小王)，(3,小张)}

函数：一个函数，是从一个映射(对应关系)产生的一种作用，称学生姓名小王在函数学号=将学生姓名变成学号作用(姓名)(简称函数f)的作用下，变成了2。称在这种作用中，学生姓名为自变量(因)，称学号为因变量(果)。

  函数一词的由来(老实说，改成作用更好)：函数，最早由中国清朝数学家李善兰翻译，出于其著作《代数学》。之所以这么翻译，他给出的原因是“凡此变数中函彼变数者，则此为彼之函数”，也即函数指一个量随着另一个量的变化而变化，或者说一个量中包含另一个量。从中可以看出，函数是指代因变量，表示因变量是含有自变量的变数，故而我们常称在作用y=5x中，y是x的一个函数。

  比较美的表述：我们说，自变量x经过f()映射作用后得到函数y，即y=f(x)。

作用(fuction)的严格定义

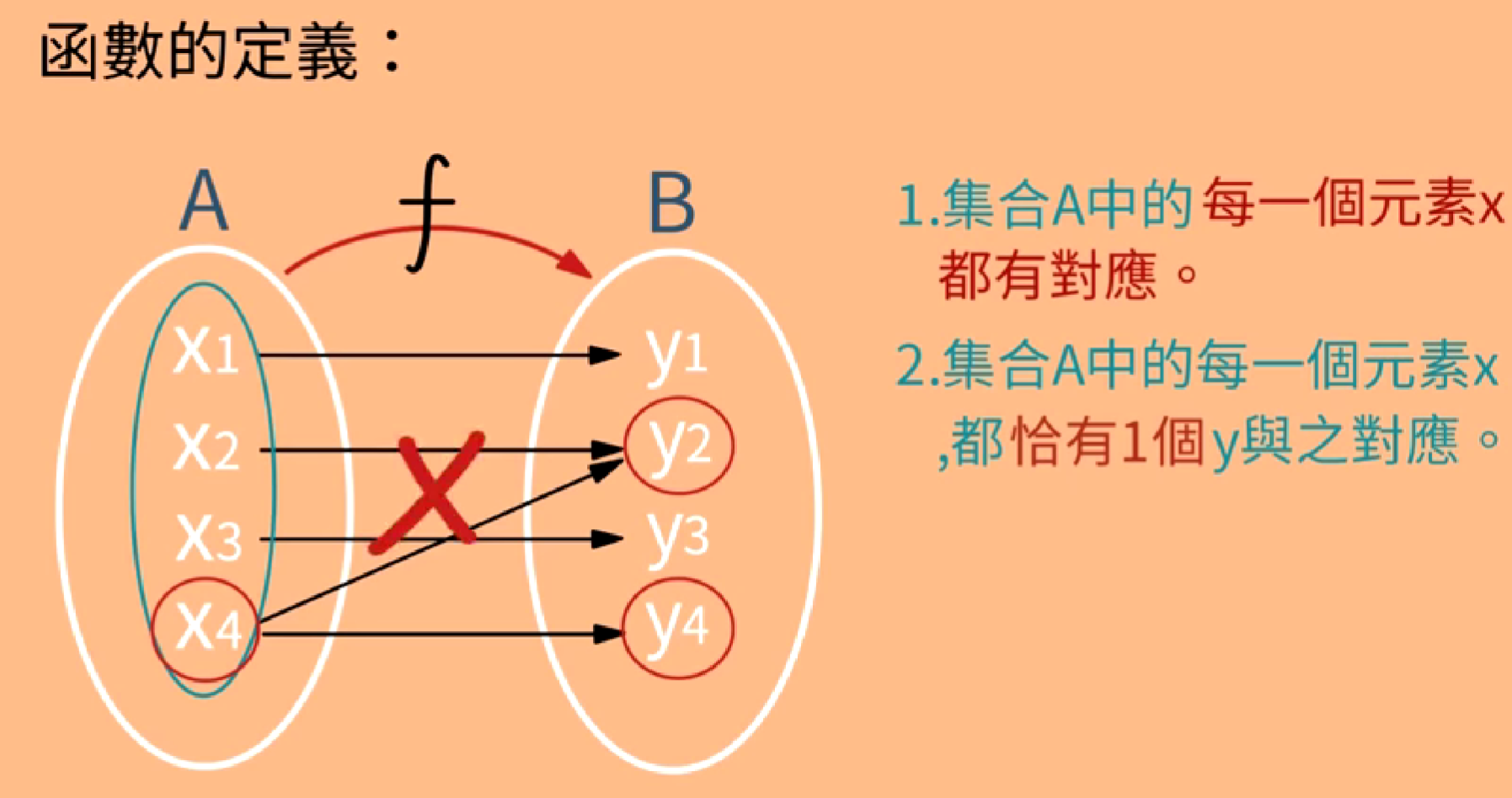
image-20211215165737479

集合A中的每一个元素x都有y对应

集合A中的每一个元素x，都恰有一个y与之对应

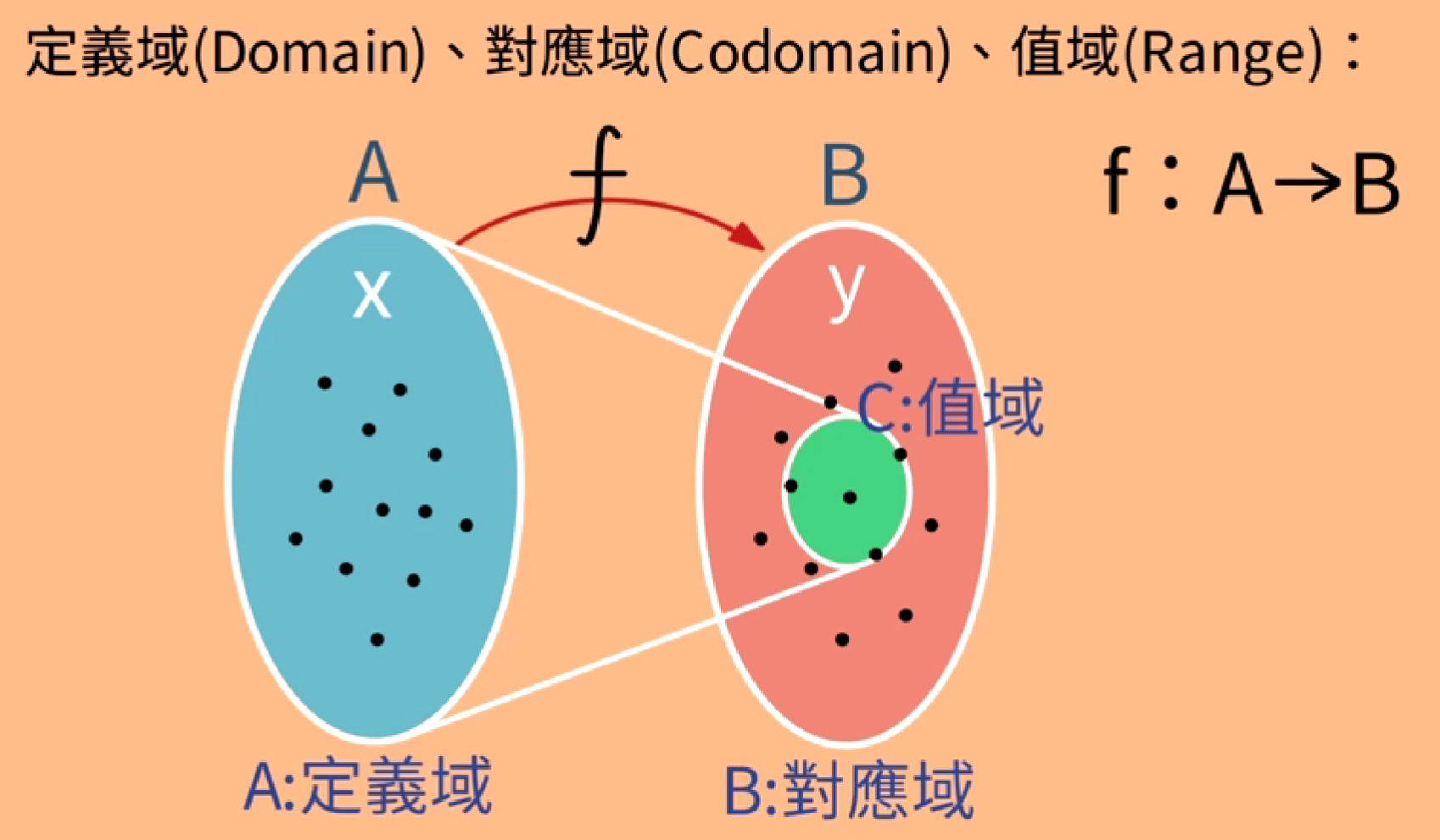
image-20211215165850772

从定义域domain出发，在对应域codomain中，对应出值域Range

一些名词

实\实值函数

值域元素都是实数的函数

集函数

定义域元素为集合的函数

单值函数

若对定义域每一个自变量x，其对应的函数值f(x)是唯一的，则称f(x)是单值函数。这也是函数的定义