无题

title: 特征函数
description: 随机过程的特征函数，到底是什么呢？怎么诞生的？有什么用？
abbrlink: 25539
date: 2021-11-08 11:54:56
tags:
categories: 数
cover: /img/math.png

不吐不快

随机过程的授课，教材，完全是一坨屎，知识出现了巨大的断层。

微积分，线性代数完全像空中楼阁，一捅就破。

人的脑子从来是从直观理解抽象(抽之于象)的，编写教材的人，授课的人，相关的人，应该好好反思自己到底在做什么。

为什么把美妙宝贵的经验模型印刷成/传授成无用的垃圾，丑陋的负担，面目可憎的东西。

将妙趣横生，令人拍声叫好的思维果实，塑造成毫无美感的恶心的东西，也是离谱了。

烂尾宣告

烂尾了，现阶段理解不了。从泰勒级数，微分的基础：用极限求导，指数函数求导诞生自然常数e，虚数单位i，复杂数a+bi，泰勒级数推导出的欧拉公式，到对随机变量的矩的理解，特征函数包含了随机变量的所有矩，最后倒在傅里叶变换。

随机变量和分布函数

  随机变量是函数，其反应的映射关系是从随机试验的样本空间中的样本，映射到值域中的一个值。

  累积概率分布函数F(x)=P{X≤x} （某事件概率=符合该事件的样本数/样本总数）用来研究随机试验样本或结果的分布情况(概率)。

  概率密度函数：对应于离散型随机变量的分布律，展示了每一个值域中的值出现的概率，概率密度展示了连续型随机变量每一个值域中的值出现的概率。

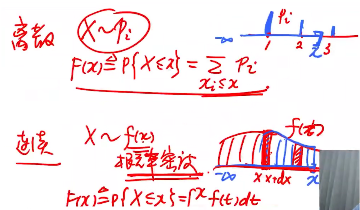
  在物理中，密度是质量m/体积v，表示单位体积的平均质量。对应到概率论中，密度是累加的概率P/一段值域，表示这单位区域长度上的平均概率，对F(x)求导，导数是某点附近的平均概率。可以用∫f(x)dx求累积概率分布函数F(x)。

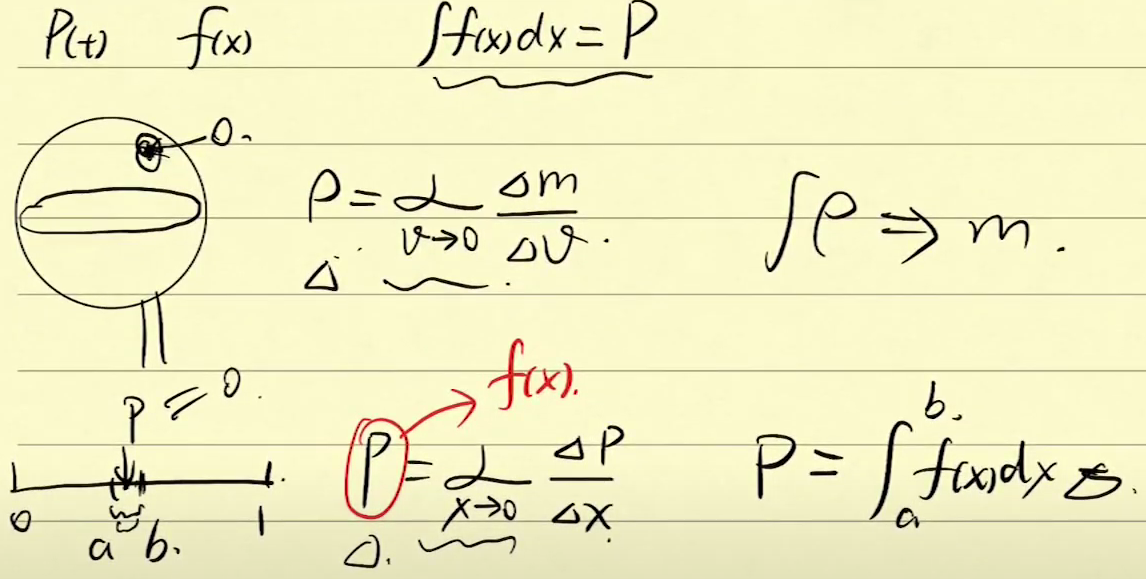
结论

特征函数是随机变量的分布的另一种表现形式。

泰勒级数

参考妈咪说视频，两个函数，起点一样，各阶导数(函数关于自变量的变化率，函数关于自变量的变化率的变化率…)都一样，就认为这两个函数一样。

亲民的函数如多项式函数

y=x

y=x^3+x^2+5x+6

给一个x值，很快能算出对应的y值

多项式：自变量和常数通过加减乘以及自然数的幂次方运算得到的代数表达式

不亲民的函数如三角函数和e^x

y=sinx

y=cosx

y=e^x

这类函数你就不能很快的得到函数值，不能够快速求值，就比较讨厌

根据泰勒级数可知，两个函数f(x)，g(x)的各阶导数相等的越多，那么这两个函数越相似。

不亲民的函数能否用多项式进行表达呢？

引子

速度是路程关于时间的变化率，加速度是速度关于时间的变化率，加速度的加速度是加速度关于时间的变化率，…, 变化率也叫导数。

两个小人从同一起点沿同一直线，如果想走的一模一样，其初始速度，加速度，加速度的加速度, … 也就是n阶导数都要一样。

用多项式拟合不亲民的函数，如果无穷项，那就是一模一样

假设f(x)=e^x 或 sinx 或 cosx

g(x)=a0+a1x+a2x^2+…+anx^n

要求f(0)=g(0)=1 => a0=1，使得起点和各阶导数都相等

f’(0) = g’(0)

f’’(0)=g’’(0)

…

fn(0)=gn(0)=n!an

自然常数e，诞生自指数函数求导

参考MIT课程 highlights of calculus

参考youtube视频

https://www.youtube.com/watch?v=m2MIpDrF7Es

e的产生

人们用极限对指数函数求导发现

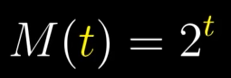
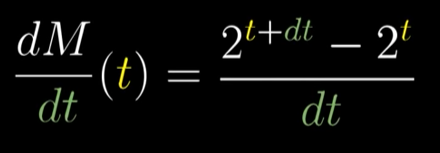
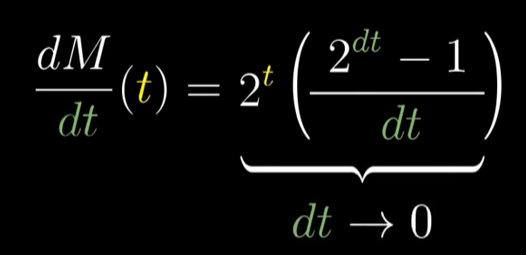
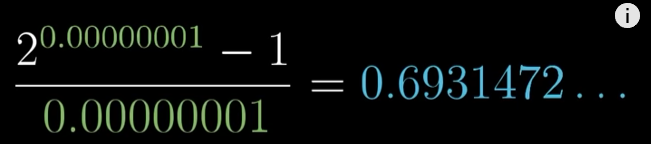
M(t)=2^t的导数，与其本身成正比，比值为一个神秘的数字0.693…

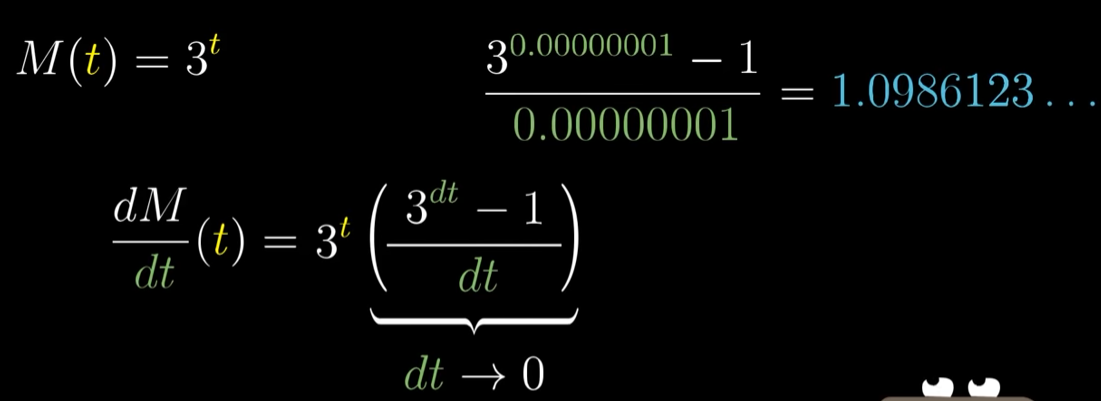
M(t)=3^t的导数，与其本身成正比，比值为一个神秘的数字1.098…

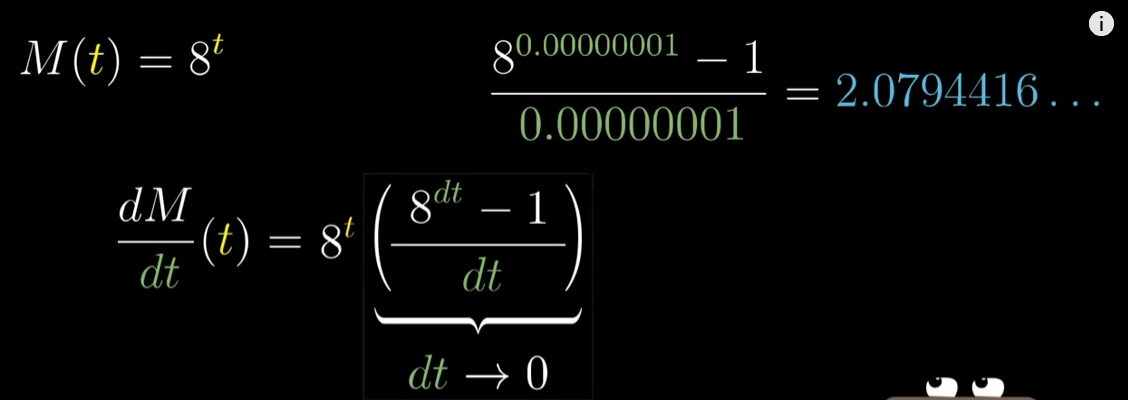
M(t)=8^t的导数，与其本身成正比，比值为一个神秘的数字2.079…

是否有一个底数，使得其指数函数的导数与自身相等？定义其为e

根据e^t的导数等于自身的性质，求e

根据性质，直接用泰勒级数逼近e^x

$$e^x=1+x+{x^2\over2!}+{x^3\over3!}+{x^4\over4!}+...+{x^n\over n!}$$

当x=1时，就产生了e

微分方程：dy/dx=y 即求导数等于自身的y，y=e^x

自然对数的使用，结合链式求导规则

链式求导规则：

代数，以符号代数：

$${△z\over△y}{△y\over△x}={△z\over△x}$$

极限，△(距离)趋近无穷小

$${dz\over dy} {dy\over dx} = {dz\over dx}$$

使用自然对数换底：

如2换成e^ln(2), 2^t求导后为ln(2)e^ln(2)t = ln(2)2^t

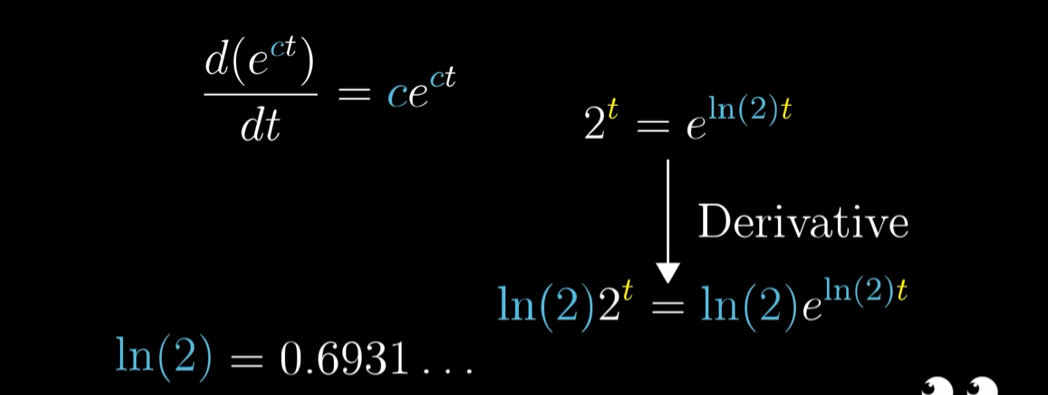
现在，指数函数求导得到的神秘系数，就是以其底数为真值的自然对数。

数系和欧拉公式

参考李永乐视频

数系

1. 自然数N：{1，2，3，…}。1+2=3对加法封闭，1-2=-1对减法不封闭
2. 整数Z：{…，-2，-1，0，1，2，…}。 对加减法封闭，2*3=6对乘法封闭，对除法不封闭2/3=?
3. 可比数Q：{x|x=p/q, p,q∈Z}。对加减乘除封闭（除数不为0），2的开方=？对开方不封闭。
4. 实数R ：用一根数轴表述，你给一个可比数，或者给一个不可比数，我都可以在数轴上找一个点。认为实数与数轴上的点一一对应。

复数

一开始人们认为2-3没有意义，后来称其结果为-1，自然数拓宽到整数。

人们又认为2/3是没有意义的，后来称其为分数(可比数)，整数拓宽带可比数。

人们又认为根号2是没有意义的，后来称其为不可比数，可比数拓宽到实数。

现在，人们认为方程x^2=-1的解是没有意义的，也许它是有意义的，称其解为复数。

虚数

i^2=-1 => i=根号-1，i就是虚数单位

i^1=i，i^2=-1，i^3=-i，i^4=1

复数

形如a+bi的数，其中a和b都是实数。

复数的概念可以在一个平面上表示，横轴表示实数轴，数轴为虚数轴。

对于复数，加减乘除或者是实数次幂都是封闭的。

欧拉公式

问题来了，有人问一个数的复数次幂，比如2^i是什么呢？

于是欧拉提出了欧拉公式：e^iθ=cosθ+isinθ

欧拉恒等式：令θ=π，e^iπ=-1，即e^iπ+1=0

最美公式

人们说欧拉恒等式是最美的公式，因为它联系了自然界最重要的五个数：e，π，1，0，i

欧拉公式的证明

可以用泰勒展开

$$e^x=1+x+{x^2\over2!}+{x^3\over3!}+{x^4\over4!}+...+{x^n\over n!}$$ $$sinx=x-{1\over3!}x^3+{1\over5!}x^5-{1\over7!}x^7+...$$ $$cosx=1-{1\over2!}x^2+{1\over4!}x^4-{1\over6!}x^6+...$$

也可以用微分方程

欧拉公式的应用

可以把复数形式变成指数形式

概率论中的矩

力矩

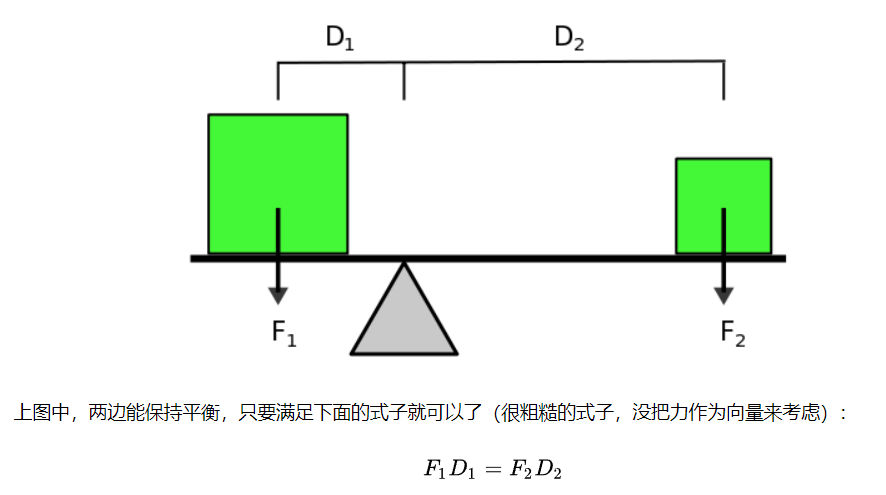
概率论中的矩

彩票问题

每一张中奖率如下

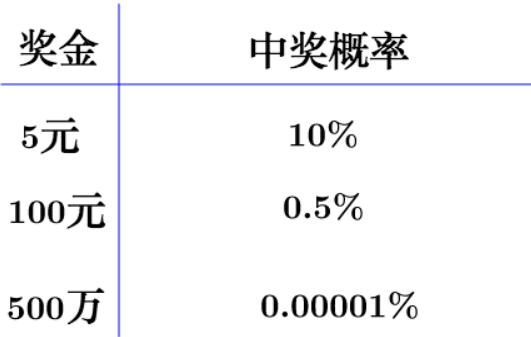
画成概率分布图

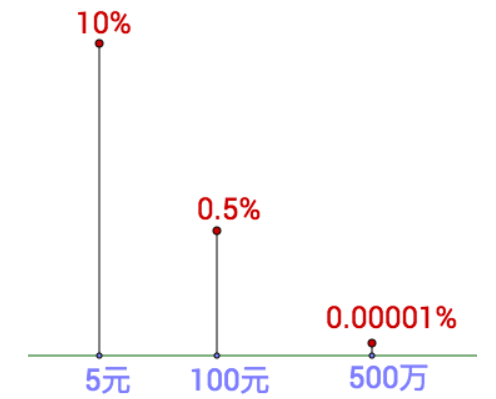
把0.00001%概率的500万，称一下，等同于概率为1的0.5

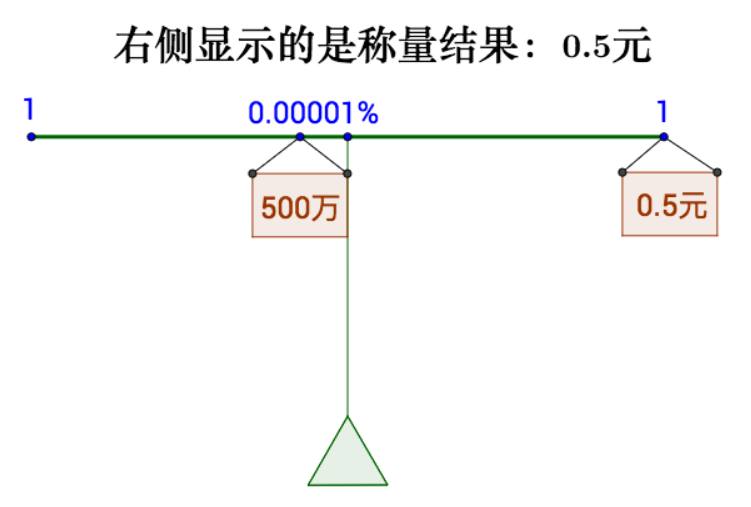
把可能中奖的结果称一下，等同于概率为1的1.5

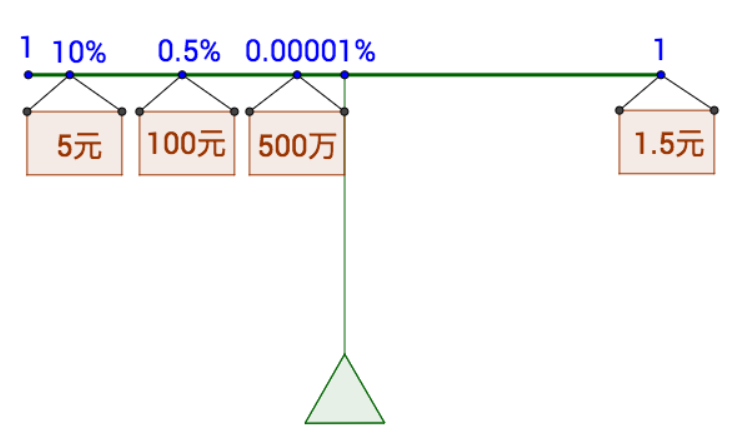
实际上，如果都能卖完，一张彩票值1.5元，它卖2元它就赚。

矩

我们上面算的，实际上是期望E[x]=∑pixi，其实这就是矩

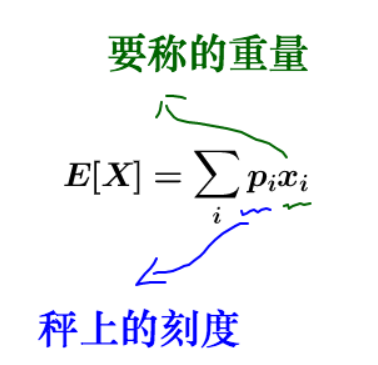
因为x是一次幂，所以也称一阶矩

方差D(x)=E[(X-μ)^2] = ∑pi(xi-μ)^2，所以方差也称为二阶矩。

矩是对试验及其对应的随机变量的一种刻画

直觉上可以有以下推论（其实还是有条件的，这里先忽略这些严格性，在实际应用中如下思考问题不大）：

各阶矩相等=>各个特征相等=>分布相同

随机变量的特征函数

随机变量X的特征函数定义为：

$$\psi_X(t)=E[e^{itX}]$$

为什么这么定义呢？首先，e^itX的泰勒展开式为：

$$e^{itX}=1+{itX\over1}-{t^2X^2\over2!}-{it^3X^3\over3!}+...+{(it)^nX^n\over n!}$$

代入可以推出

$$\psi_X(t)=E[e^{itX}]=1+{itE[X]\over1}-{t^2E[X^2]\over2!}-{it^3E[X^3]\over3!}+...+{(it)^nE[X^n]\over n!}$$

原来特征函数包含了分布函数的所有矩，也就是包含了分布函数的所有特征。

有数学家这么形同生成函数（特征函数是生成函数的一种）：

A generating function is a clothesline on which we hang up a sequence of numbers for display. 生成函数是用来展示一串数字的晾衣架。

特征函数确实像把各阶矩串在绳子上：

特征函数就是随机变量X的分布的另一种描述方式。

傅里叶变换

参考 李永乐视频

参考 知乎文章 傅里叶分析之掐死教程（完整版）更新于2014.06.06 - 知乎 (zhihu.com)

傅里叶系列（一）傅里叶级数的推导 - 知乎 (zhihu.com)

变换

向量 <-> 点坐标，正交基

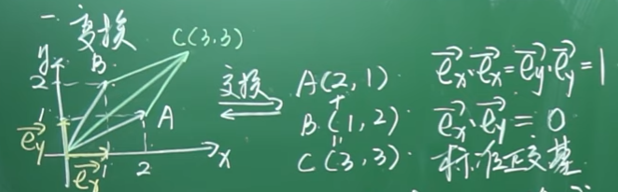
描述规律振动现象的数学语言-三角函数

如物体挂在弹簧上作简谐振动、单摆振动、无线电电子振荡器的电子振荡等，大多可以表述为：

$$f(t)=Asin(\omega t+\psi)$$

其中，t表示时间，A表示振幅，ω表示角频率(是对旋转快慢的度量)，ψ表示初相(与考察时设置的原点位置有关)

傅里叶级数的提出

然而，世界上许多周期信号并非正弦函数那么简单，如方波、三角波等。傅里叶就想，能否用一系列的三角函数Ansin(nωt+ψ)之和来表示较复杂的周期函数f(t)呢。

于是，1807年，傅里叶提出(据说是傅里叶解热方程和弦振动导出的)：

$$f(t)=A0+\sum_{n=1}^\infty A_nsin(n\omega t + \psi_n) \qquad(2)$$

这里，t是变量，其他都是常量。傅里叶是想把一个周期为T的函数表示成周期为T,2T,3T,4T,… 的正弦函数的线性叠加，一大堆正弦函数有不同的振幅，周期或者说频率，初相角，常数系数。n是从1到无穷大，这是一个无穷级数。

这里强调一下，傅里叶级数中对不同频率的波有一个要求就是给定一个初始的频率ω0，2π\ω0就是f(t)的周期，之后的角频率必须是ω0的整数倍，这就是DFT(Discrete Fourier Transform，DFT)中的角频率取值的规则

傅里叶对式2使用和角公式作变形：

$$A_nsin(n\omega t+\psi_n)=A_nsin\psi_ncos(n\omega t)+A_ncos\psi_nsin(n\omega t) \qquad(3)$$

整合常数项，记

$$a_n=A_nsin\psi_n，b_n=A_ncos\psi_n$$

这样公式3就可以写成如下形式：

$$f(t)=A_0+\sum_{n=1}^\infty[a_ncos(n\omega t)+b_nsin(n\omega t)] \qquad (4)$$

我们只要解出A0，an，bn就可以得到周期函数f(t)的傅里叶级数

麦克劳林公式中的待定系数法

这里为求A0，an，bn提供思路：

泰勒级数即为任意一个函数都可以用一个多项式来逼近，记为：

$$f(x)=A+Bx+Cx^2+Dx^3+...$$

那么，麦克劳林令：

$$f'(x)=B+2Cx+3Dx^2+...$$ $$f''(x)=2CX+6Dx+...$$ $$......$$

令x=0，可知

$$A=f(0)$$ $$B=f'(0)$$ $$C=f''(0)/2!$$ $$D=f'''(0)/3!$$

即

$$N=f^n(x)/n!$$

而三角函数在一个周期内的积分(求被积函数与横坐标轴围成的面积，也是求还原后函数的值的变化量)为0：

三角函数的正交性

这是为下一步傅里叶级数展开时所用积分的准备知识：

一个三角函数系：1,cosx,sinx,cos2x,sin2x,…,cosnx,sinnx,…如果这一堆函数(包括常数1)中任何两个不同函数的乘积在区间[-π，π]上的积分为0，就说三角函数系在区间[-π，π]上正交，即有如下式子：

$$\int_{-\pi}^{\pi}cosnxdx=0 \quad(n=1,2,3,...)$$ $$\int_{-\pi}^{\pi}sinnxdx=0 \quad(n=1,2,3,...)$$ $$\int_{-\pi}^{\pi}sinkx·cosnxdx=0 \quad(k,n=1,2,3,...)$$ $$\int_{-\pi}^{\pi}coskx·cosnxdx=0 \quad(k,n=1,2,3,...;k\neq n)$$ $$\int_{-\pi}^{\pi}sinkx·sinnxdx=0 \quad(k,n=1,2,3,...;k\neq n)$$

以上各式在区间[-π,π]的定积分均为0，第1式第2式可视为三角函数cos和sin与1相乘的积分；第3-5式则为sin和cos的不同组合相乘的积分公式。除了这5个式子外，不再有其他组合。但第3式中，k与n可以相等，相等时也是二个不同函数。

$$coskx·cosnx={1\over2}[cos(k+n)x+cos(k-n)x]$$ $$sinkx·sinnx=-{1\over2}[cos(k+n)x-cos(k-n)x]$$ $$sinkx·cosnx={1\over2}[sin(k+n)x+sin(k-n)x]$$

计算第4式的定积分结果为0,3和5式方法相同

$$\int_{-\pi}^\pi coskx·cosnxdx = {1\over2}\int_{-\pi}^\pi[cos(k+n)x+cos(k-n)x]dx = {1\over2}[{sin(k+n)x\over k+n}+{sin(k-n)x\over k-n}]|_{-\pi}^\pi = {1\over2}[0+0]=0$$

现在，我们知道三角函数系：1,cosx,sinx,cos2x,sin2x,…,cosnx,sinnx,…这一堆函数(包括常数1)中任何两个不同函数的乘积在区间[-π，π]上的积分为0

函数展开成傅里叶级数

前面提出的傅里叶级数：

$$f(t)=A_0+\sum_{n=1}^\infty[a_ncos(n\omega t)+b_nsin(n\omega t)] \qquad (4)$$

对4式从[-π,π]积分，得

$$\int_{-\pi}^{\pi}f(t)dt=\int_{-\pi}^\pi A_0dt+ \int_{-\pi}^\pi\sum_{n=1}^\infty[a_ncos(n\omega t)+b_nsin(n\omega t)]dt$$ $$=\int_{-\pi}^{\pi}A_0dt+0=A_0t|_{-\pi}^\pi$$ $$=(\pi-(-\pi))A_0=2\pi A_0$$

求得A0

$$A_0={1\over2\pi}\int_{-\pi}^{\pi}f(t)dt$$

用coskωt乘4式的两边得

$$f(t)cos(k\omega t)=A_0cos(k\omega t)+\sum_{n=1}^\infty[a_ncos(n\omega t)cos(k\omega t)+b_nsin(n\omega t)cos(k\omega t)]$$

对上式两边同时从-π到π积分

$$\int_{-\pi}^{\pi}f(t)cos(k\omega t)dt = A_0\int_{-\pi}^{\pi}cos(k\omega t)dt+\sum_{n=1}^\infty[a_n\int_{-\pi}^{\pi}cos(n\omega t)·cos(k\omega t)+b_n\int_{-\pi}^{\pi}sin(n\omega t)·cos(k\omega t)]dt$$

根据三角函数的正交性，仅当k=n时，右边有不为0的积分项，即

$$\int_{-\pi}^{\pi}cos(k\omega t)f(t)=a_n\int_{-\pi}^{\pi}cos^2(n\omega t)dt$$ $$={a_n\over 2}\int_{-\pi}^{\pi}(1+cos2n\omega t)dt \qquad(半角公式)$$ $$={a_n\over 2}(\int_{-\pi}^{\pi}1dt+\int_{-\pi}^{\pi}cos2n\omega tdt) \qquad(后一项三角函数积分为0)$$ $$={a_n\over2}·2\pi=a_n\pi$$

解得

$$a_n={1\over\pi}\int_{-\pi}^{\pi}cos(n\omega t)·f(t)dt \qquad(k=n)$$

同理，用sin(kωt)乘4式两边得：

$$b_n={1\over\pi}\int_{-\pi}^{\pi}sin(n\omega t)·f(t)dt$$

我们发现A0的分母为2π，而an和bn的分母为π，为了统一分母，能够将a0用an表示，我们令a0=2A0 有：

$$a_0={1\over\pi}\int_{-\pi}^{\pi}f(t)dt$$

推导的时候假设T=2π，然而T可以为任何长度的周期，将T=2π带进an，bn的表达式中

汇总得：

$$a_n={2\over T}\int_{t_0}^{t_0+T}cos(n\omega t)·f(t)dt$$ $$b_n={2\over T}\int_{t_0}^{t_0+T}sin(n\omega t)·f(t)dt$$

傅里叶级数的指数形式

根据欧拉公式，有

$$cos(n\omega t)={1\over 2}(e^{-in\omega t}+e^{in\omega t})$$ $$sin(n\omega t)={j\over 2}(e^{-in\omega t}-e^{in\omega t})$$

代入傅里叶级数得：

$$f(t)={a_0\over 2}+\sum_{n=1}^\infty[a_n{e^{in\omega t}+e^{-in\omega t}\over 2}+ib_n{e^{-in\omega t}-e^{in\omega t}\over 2}]$$ $$={a_0\over 2}+\sum_{n=1}^\infty[{a_n-ib_n\over 2}e^{in\omega t}+{a_n+ib_n\over 2}e^{-in\omega t}] \qquad (5)$$

将an,bn的表达式代入得

$${a_n-ib_n\over 2}={1\over T}[\int_{t_0}^{t_0+T}f(t)cos(n\omega t)dt-i\int_{t_0}^{t_0+T}f(t)sin(n\omega t)dt]$$ $$={1\over T}\int_{t_0}^{t_0+T}f(t)[cos(n\omega t)-isin(n\omega t)]dt$$ $$={1\over T}\int_{t_0}^{t_0+T}f(t)e^{-in\omega t}dt$$

同理可得：

$${a_n+ib_n\over2}={1\over T}\int_{t_0}^{t_0+T}f(t)e^{in\omega t}dt$$

将两式代入5式得

$$f(t)={1\over T}\int_{t_0}^{t_0+T}f(t)dt+{1\over T}\sum_{n=1}^\infty[\int_{t_0}^{t_0+T}f(t)e^{-in\omega t}dt·e^{in\omega t}+\int_{t_0}^{t_0+T}f(t)e^{in\omega t}dt·e^{-in\omega t}]$$ $$={1\over T}\int_{t_0}^{t_0+T}f(t)dt+{1\over T}\sum_{n=1}^\infty\int_{t_0}^{t_0+T}f(t)e^{-in\omega t}dt·e^{in\omega t}+{1\over T}\sum_{n=-1}^{-\infty}\int_{t_0}^{t_0+T}f(t)e^{-in\omega t}dt·e^{in\omega t}$$ $$={1\over T}\sum_{n=-\infty}^{+\infty}\int_{t_0}^{t_0+T}f(t)e^{-in\omega t}dt·e^{in\omega t} \qquad (6)$$ $$注：当n=0时，{1\over T}\int_{t_0}^{t_0+T}f(t)e^{-in\omega t}dt·e^{in\omega t}={1\over T}\int_{t_0}^{t_0+T}f(t)dt$$

傅里叶变换

傅里叶级数只能处理周期函数，傅里叶变换可以处理非周期函数。

仔细研究6式 , ω角频率是2π/T的简写，是常量，当周期无穷大时，ω无穷小，而从频率的角度看一大堆正余弦函数，nω是一个变量表示不同的频率：

令

$$\omega_x={2\pi\over N}·n \quad(N\rightarrow+\infty,N∈Z)$$ $$F(\omega_x)=\int_{t_0}^{t_0+T}f(t)e^{-i\omega_xt}dt$$

有

$$f(t)={1\over T}\sum_{n=-\infty}^{+\infty}\int_{t_0}^{t_0+T}f(t)e^{-in\omega t}dt·e^{in\omega t}$$ $$={1\over T}\sum_{n=-\infty}^{n=\infty}[F(\omega_x)·e^{i\omega_xt}]$$

根据积分表达式的黎曼和表达式

$$\int_a^bf(x)dx=\lim_{h->0}\sum_{n=0}^{(b-a)/h}f(a+n·h)·h$$ $${1\over T}\sum_{n=-\infty}^{n=\infty}[F(\omega_x)·e^{i\omega_xt}]={N\over 2\pi·T}\sum_{n=-\infty}^{n=+\infty}[F(\omega_x)·e^{i\omega_xt}·{2\pi\over N}]$$ $$={N\over 2\pi·T}\int_{-\infty}^{+\infty}F(\omega_x)·e^{i\omega_xt}·{2\pi\over N}d\omega_x$$

令T->N，即可得到一个标准的傅里叶变换公式：

$$f(t)={1\over2\pi}\int_{-\infty}^{+\infty}F(\omega_x)e^{i\omega_xt}d\omega_x \qquad (7)$$

其中

$$F(\omega_x)=\int_{t_0}^{t_0+T}f(t)e^{-i\omega_xt}dt \qquad(8)$$

已知f(t),我们可以通过8式从时域函数f(t)中摘出频率ωn即ωx，得到频域函数的值F(ωx)

通过7式将频域函数F(ωx)原成原来的时域信号f(t)。

傅里叶变换分析

傅里叶变换，把一个信号拆成一大堆不同频率的正弦信号，实部为振幅，虚部为相位。

傅里叶逆变换，把一大堆正弦信号逆变回原来的信号。

对于傅里叶级数和傅里叶变换中实部和虚部(复数)的理解

To Do

特征函数是概率密度函数f(x)的共轭傅里叶变换

特征函数相当于换了一个坐标系

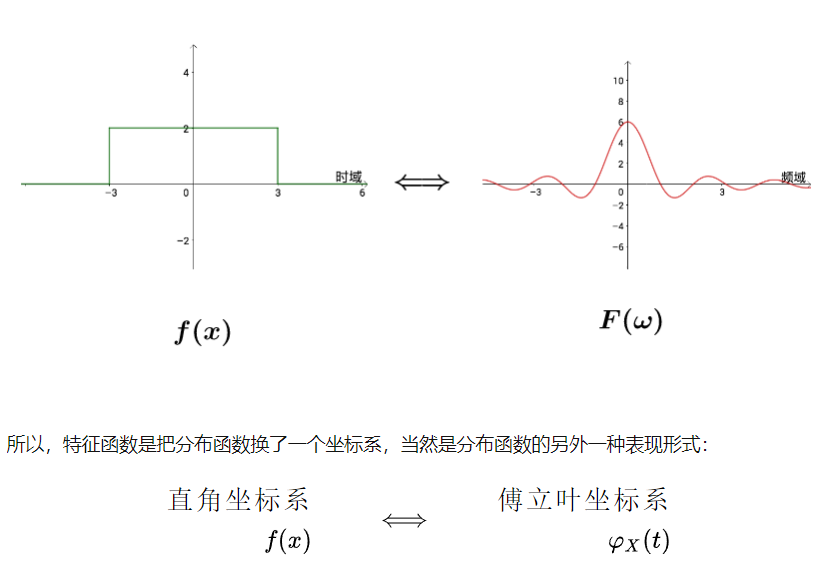
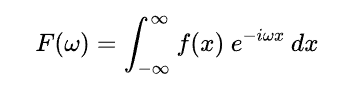
特征函数的好处