自然常数e

泰勒级数

参考妈咪说视频，两个函数，起点一样，各阶导数(函数关于自变量的变化率，函数关于自变量的变化率的变化率…)都一样，就认为这两个函数一样。

亲民的函数如多项式函数

y=x

y=x^3+x^2+5x+6

给一个x值，很快能算出对应的y值

多项式：自变量和常数通过加减乘以及自然数的幂次方运算得到的代数表达式

不亲民的函数如三角函数和e^x

y=sinx

y=cosx

y=e^x

这类函数你就不能很快的得到函数值，不能够快速求值，就比较讨厌

根据泰勒级数可知，两个函数f(x)，g(x)的各阶导数相等的越多，那么这两个函数越相似。

不亲民的函数能否用多项式进行表达呢？

引子

速度是路程关于时间的变化率，加速度是速度关于时间的变化率，加速度的加速度是加速度关于时间的变化率，…, 变化率也叫导数。

两个小人从同一起点沿同一直线，如果想走的一模一样，其初始速度，加速度，加速度的加速度, … 也就是n阶导数都要一样。

用多项式拟合不亲民的函数，如果无穷项，那就是一模一样

假设f(x)=e^x 或 sinx 或 cosx

g(x)=a0+a1x+a2x^2+…+anx^n

要求f(0)=g(0)=1 => a0=1，使得起点和各阶导数都相等

f’(0) = g’(0)

f’’(0)=g’’(0)

…

fn(0)=gn(0)=n!an

自然常数e，诞生自指数函数求导

参考MIT课程 highlights of calculus

参考youtube视频

https://www.youtube.com/watch?v=m2MIpDrF7Es

e的产生

人们用极限对指数函数求导发现

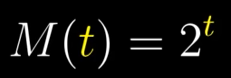
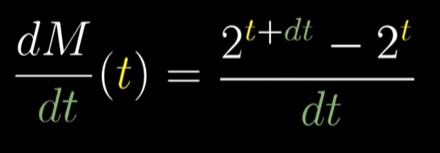
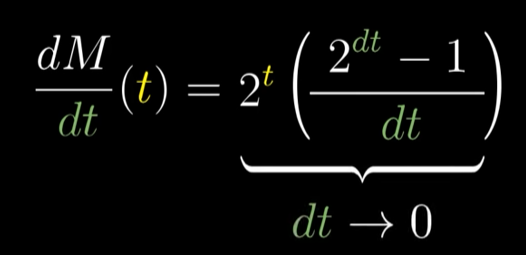
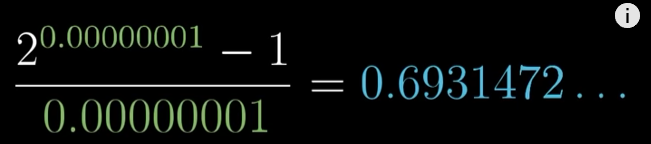
M(t)=2^t的导数，与其本身成正比，比值为一个神秘的数字0.693…

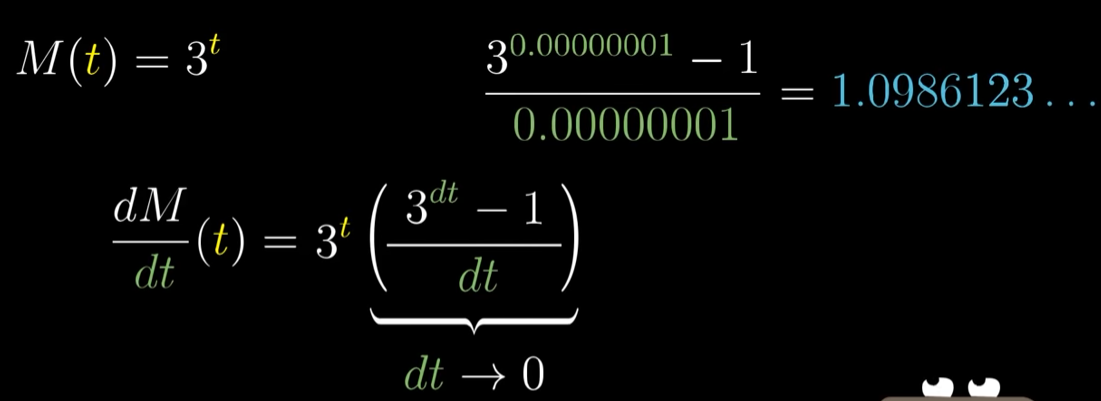
M(t)=3^t的导数，与其本身成正比，比值为一个神秘的数字1.098…

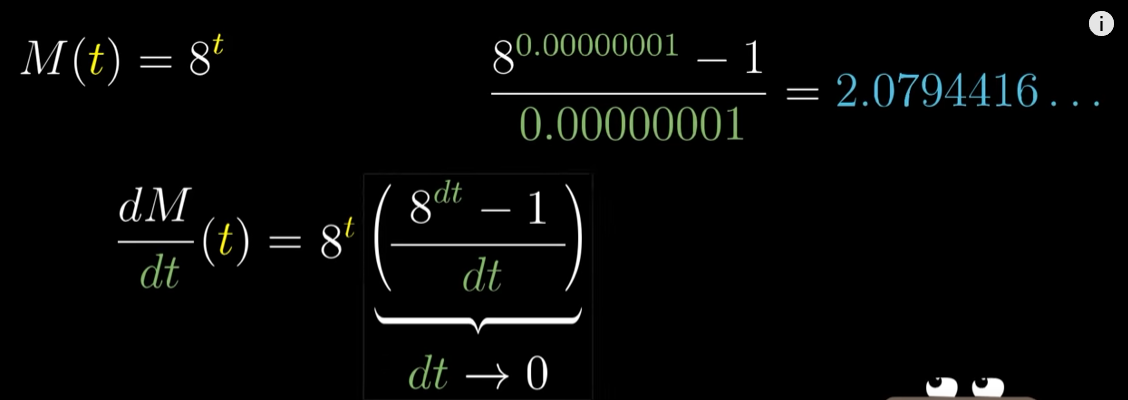
M(t)=8^t的导数，与其本身成正比，比值为一个神秘的数字2.079…

是否有一个底数，使得其指数函数的导数与自身相等？定义其为e

根据e^t的导数等于自身的性质，求e

根据性质，直接用泰勒级数逼近e^x

$$e^x=1+x+{x^2\over2!}+{x^3\over3!}+{x^4\over4!}+...+{x^n\over n!}$$

当x=1时，就产生了e

微分方程：dy/dx=y 即求导数等于自身的y，y=e^x

自然对数的使用，结合链式求导规则

链式求导规则：

代数，以符号代数：

$${△z\over△y}{△y\over△x}={△z\over△x}$$

极限，△(距离)趋近无穷小

$${dz\over dy} {dy\over dx} = {dz\over dx}$$

使用自然对数换底：

如2换成e^ln(2), 2^t求导后为ln(2)e^ln(2)t = ln(2)2^t

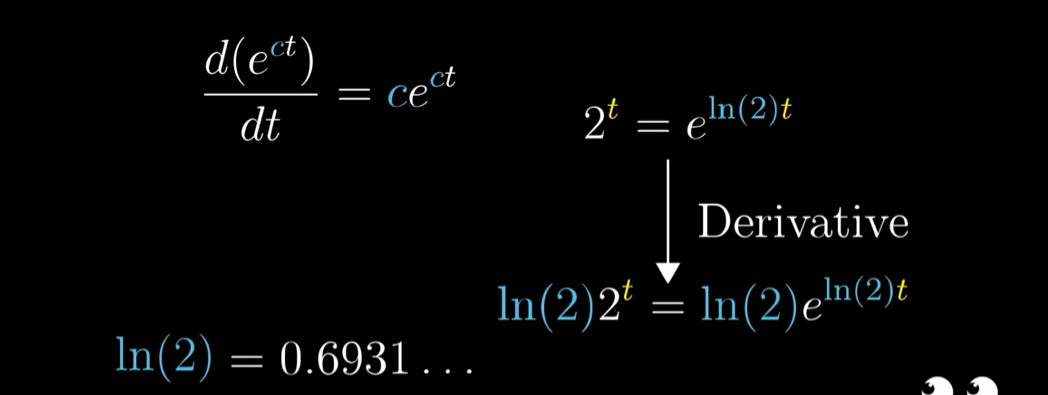
现在，指数函数求导得到的神秘系数，就是以其底数为真值的自然对数。

证明复利公式的极限是e,用到洛必达法则

$$证明：y=f(n)=\lim_{n->\infty}(1+{1\over n})^n=e$$

两边经自然对数函数作用，利用对数函数的规则作变形

$$lny=\lim_{n->\infty}ln[(1+{1\over n})^n]=\lim_{n->\infty}nln(1+{1\over n})$$

令n=1/x，因为n->∞，所以x->0

$$lny=\lim_{x->0}{ln(1+x)\over x}$$

根据反函数性质，结合链式求导法则，得到lny的导数:

反函数的性质：

$$ln(e^x)=x$$

两边求导：

$${dlny\over dy}{de^x\over dx}=1$$ $${dlny\over dy}={1\over e^x}={1\over y}$$ $$故 lnx的导数为{1\over x}$$

使用洛必达法则

$${lny}=\lim_{x->0}{\ {1\over 1+x}\over 1\ }=1$$

故y=e，即：

$$\lim_{n->\infty}(1+{1\over n})^n=e$$