试验与活动

首先理解这一点，活动是每天事件上所发生的一切事，活动必然有参与活动的单位或称个体与活动内容，经活动内容的作用，活动单位出现某种状态，称为事件。活动单位如一条鱼，一个网络包，一个骰子。活动内容是作用在活动单位上的动作，如养一条鱼，发一个网络包，投一个骰子。事件如鱼死，鱼活，网络包丢了，骰子为1。试验是被人类观测的，用于总结规律的活动。其试验单位称为样本点。

人类从多次大样本的试验中总结出，符合某事件的样本点数/样本点总数为一个稳定的比例。称为该试验中某事件发生的概率。同时这个经验得出的概率可以用于推测于类似的活动中，符合某事件的样本点数目，我们认定概率就是类似活动中某事件发生的比例，已知样本点总数，从而推测出类似活动中，符合某事件样本点的数目。

所以说，概率是从大样本试验中来，作用到多个体活动上去。但是，如果作用到单个体活动上呢？为此我们为单个体活动开辟一个活动结果空间。对于硬币类，骰子类活动，它们的活动结果等可能，活动结果空间具有实际意义，如{正，反}，{1,2,3,4,5,6}。可是对发一个网络包，养一条鱼这样的但个体活动而言，活动结果不是等可能的，它们的活动结果空间包含的是虚构出来的等可能活动结果。

多样本试验得到概率

有一个养鱼人的人，发现三种味道鲜美的新鱼群，分别是白鱼，红鱼，黑鱼。一开始都有100条，养鱼人开始养鱼。

第一季度，白鱼死了2条，红鱼死了3条，黑鱼死了5条。
第二季度，白鱼死了3条，红鱼死了4条，黑鱼死了10条。
第三季度，白鱼死了3条，红鱼死了4条，黑鱼死了5条。
第四季度，白鱼死了4条，红鱼死了4条，黑鱼死了7条。

最后，白鱼还剩88条，红鱼还剩85条，黑鱼还剩73条。这一年的成活率为如下表格所示。比例只是单纯的数值比，可以任意缩放，但最好分子分母都要是整数，看着最为亲切。此时，这些比例仅仅就是比例，从事实中诞生，用于优雅地描述今年的一个事实。

白鱼	红鱼	黑鱼
88/100	85/100	73/100

10年里，养鱼人勤勉地记录了10次三种鱼的成活率，对每一种鱼10年的10个比例求平均值。结果为：

白鱼	红鱼	黑鱼
87/100	86/100	81/100

1000年过去了，养鱼人的孩子还在养这三种鱼，并且传承了1000年的三种鱼的成活率数据，对每一种鱼1000年的1000个比例求平均值。结果为：

白鱼	红鱼	黑鱼
88/100	84/100	78/100

活动和试验：这份数据是对事实的勤勉记录，养鱼本来只是一种自然活动，但是作为人类总结规律的对象时，这些活动可被称为试验，试验是一种特殊的活动。从试验中总结出的规律，又能推测未来活动的情况。

个体空间和个体：活动中所有个体的集合称为个体空间，活动中的一个单位称为个体。

样本空间和样本点：试验中的观测单位的集合称为样本空间，一个观测单位称为样本点。

某种事件：某个个体或样本点出现可能的状态，称为某种事件。比如人踩人事件，鱼活着事件。

试验得出活动中出现某种事件概率：我们称经过多次大样本试验得出的，出现某种状态的样本数与样本总数的，稳定的比率为该类活动某种事件发生的概率。可能是在观察了100亿条鱼后，人们发现88亿条鱼活了下来，符合鱼活着事件。由88亿/100亿缩放，得到88/100这个比率，我们称88/100为养鱼活动鱼存活事件发生的概率。这种稳定的比率是某种稳定的事实导致的，比如白鱼的基因最好，捕食能力最强，只有少量天敌，而且生存环境没有什么变动，所以在养鱼活动中能稳定地以88/100的比例存活。小结：活动中某事件出现的概率=符合事件的样本点数/所有样本点数

概率推测活动的某种事件的个体数：养鱼人的后代，将这一概率(多次大样本试验得到的稳定比率)当做传家宝一样代代相传着，为他们的养鱼活动提供推测。而比例是不看分母分子的规模的，对于10000条鱼，这个概率告诉他们估摸8800条能活。对于100条鱼，这个概率告诉它们，估摸88条能活。小结：活动中符合某事件的个体数=活动中某事件出现的概率*所有个体数

得出概率的试验，从分母到分子全是整数：那么对于1条鱼呢？这个概率告诉他们0.88条鱼能活？这听着怪难受的对吗？可是按照比例，这说法还真没错。但是由于概率是我们从先前的大样本试验中总结的，那些观测单位-样本，作为比例分母分子的样本数都是整数。你养100条鱼，我根据先前的经验猜测你会收获88条活鱼吃；你养1000条鱼，我根据先前的经验猜测你会收获880条活鱼吃。你养1条鱼，按照比例缩放是你会收获0.88条活鱼吃？但是对不起，0.88不是个整数，现实生活中没有0.88个鱼的概念。你也不会在某活动中观测到0.88个样本符合某事件。

单样本多次试验得到概率

目前有一种通用的说法，养一条鱼，鱼存活的概率为88/100。

这是通过进行多次单样本试验得到的概率。多次单样本试验相当于一次多样本试验。养一条鱼100次，相当于养100条鱼1次。

我们知道养一条鱼的活动结果只有2个，这鱼活着或者这鱼死了。而且如果重复多次这种活动，我们会发现鱼活着的情况比鱼死要多一些，这两种活动结果是不均等出现的。从多样本试验我们可以推测，养100条鱼，估摸能活88条。养100条鱼，就相当于进行100次养一条鱼的活动，得到100次活动结果，出现88次鱼活着结果，12次鱼死了结果。鱼活着的结果和鱼死了的结果，数量比为88:12。我们因此虚构一个养一条鱼活动的活动结果空间，称有100种结果，88种活结果，12种死结果，我们只关心这两种活动结果的数量比，而不关心88种结果到底都是啥，因为这是一个虚构的活动结果空间。

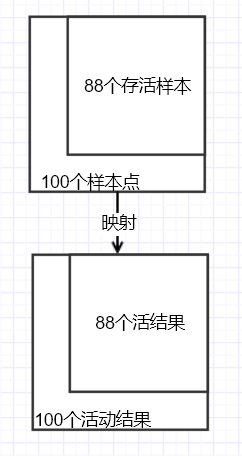
实际上，我们将100个样本的样本空间映射到了一个样本的虚构结果空间。通过这个虚构的有100个活动结果的活动结果空间，使用养鱼活动中鱼活事件的概率，推测养一条鱼活动的符合事件个体数变得有意义了，概率88/100告诉我们，养一条鱼有100种结果(此时个体变成了结果)，估摸着有88种结果符合事件鱼活着，有12种结果符合事件鱼死了。

用概率推测出来的活动结果，不是事实，完全可以看做是一次完美的试验，我们还能用这种虚构结果空间，去得到多个单样本活动的某种关系事件的概率

这样，我们如果想知道进行两次养一条鱼活动，两条鱼同时存活这一事件的概率。就可以虚构两个独立的100种结果的结果空间。两条鱼的结果空间就有100100=10000种结果(鱼1的每一种结果都对应鱼2的100种结果)。符合活着事件的结果有88\88种(鱼1的每一个活着结果都对应鱼2的88种活着结果)。将虚构结果空间看做试验样本空间，所有结果数就是样本总数，符合活着事件的结果数就是符合该事件的样本数，两一条鱼两次，两条鱼都活着的概率就是88*88/100*100。**此时，不可再用多样本试验的角度看待这个概率，因为此时事件已经是某种两次活动中单样本的关系(二元式)了。

总结

不同于抛硬币，投色子这种，天然具有多种等可能活动结果的单个体活动。对于这种天然具有多种等可能活动结果的单个体活动，它们有一个实际有意义的等可能结果空间，如{正，反}，{1,2,3,4,5,6}。

对于发送一个网络包，养一条鱼这种，不具有多种等可能活动结果的单个体活动，依据某事件的概率开辟一个活动结果空间，活动结果总数为分母，符合事件的活动结果数位分子。这个活动结果空间虽然是虚构的，但是有意义的，相当于描述了一个样本点总数为概率分母的多样本试验的情况。在虚构活动结果空间的帮助下，某事件的概率能对单个体活动中符合某事件的试验结果数做推测了。并且还可以在此之上研究多个单个体活动某种关系事件发生的概率。