导数
参考马同学的众多知乎回答
导数
积分的历史背景
17世纪,当时很重要的问题是天文学问题,其中,开普勒三定律中的第二定律:在相等时间内,太阳和运动着的行星的连线扫过的面积都是相等的。

既然有计算不规则曲线面积的需求,那么数学家就得去研究,所谓积分就是求曲线下的面积(17世纪,英文中积分”quadrature”的含义就是求面积的意思):
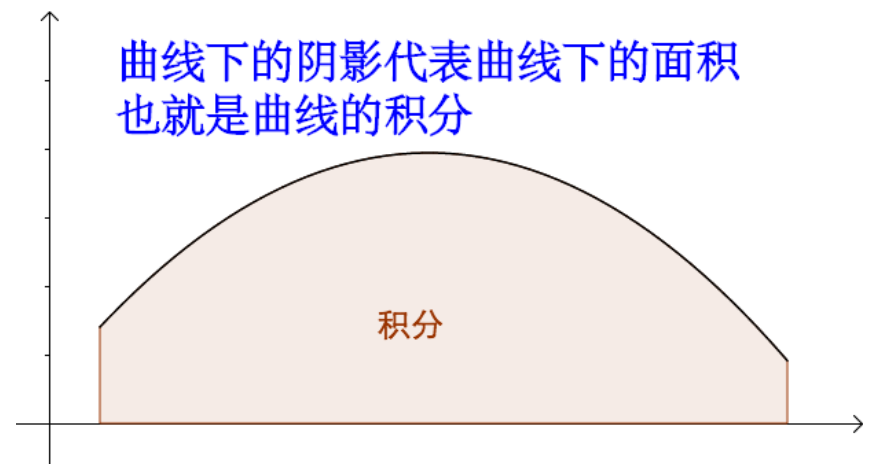
积分的思想
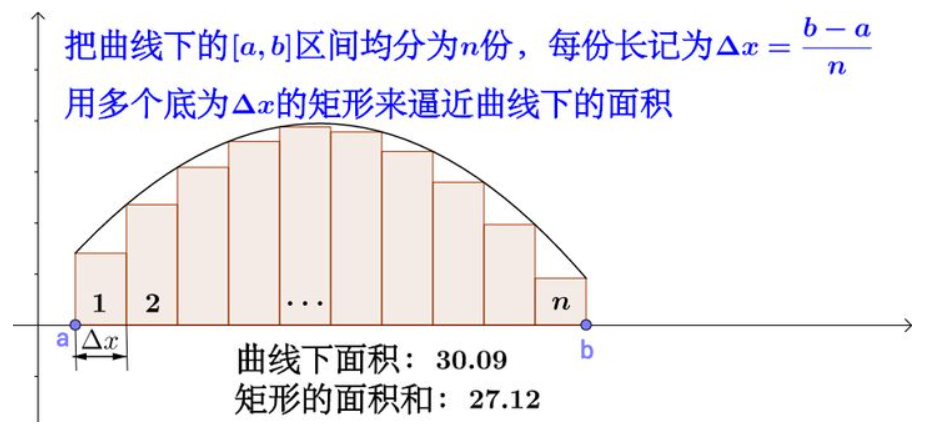
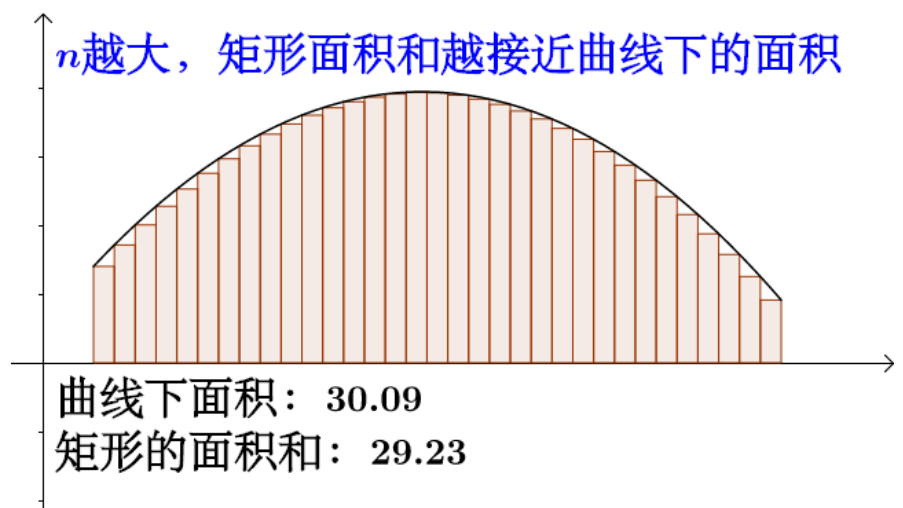
微积分:以直代曲,线性逼近
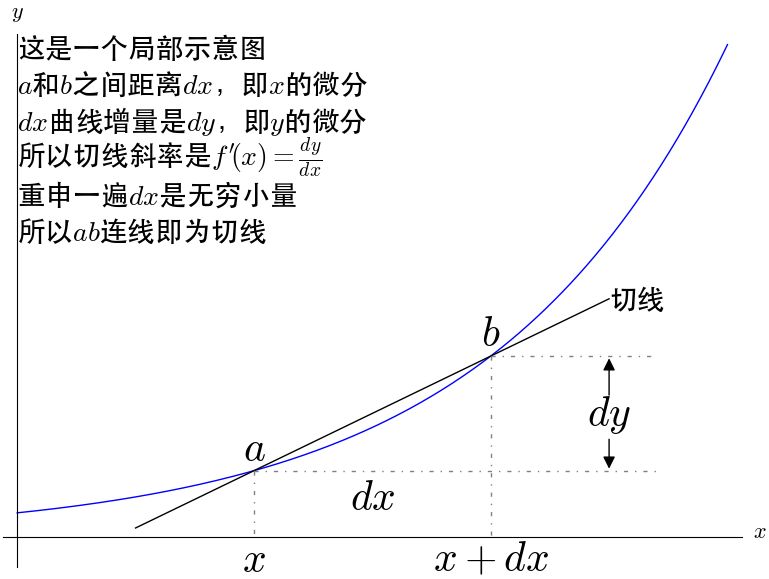
微分:无穷小量
从上图得出导数的定义,f’(x)=dy/dx, 而dx和dy被称为x和y的微分,都为无穷小量。所以导数也被莱布尼兹称为微商(微分之商)
无穷小量引发第二次数学危机
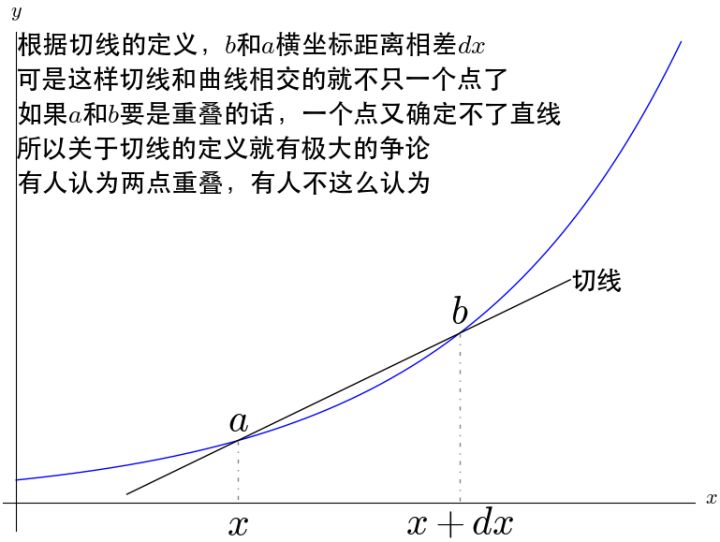
所以就切线的定义而言,微积分的基础是不牢靠的。
无穷小量的麻烦远不止这一些

基于极限重建微积分
莱布尼兹、欧拉等人都认识到无穷小量导致的麻烦,一直想要修补。但是这个问题等到200年后,19世界极限的概念清晰之后才得到解决。
极限
如何描述△x无限接近于0?
△x无限接近于0,但不能为0,否则以0为底边长的矩形面积为0,无穷多个0相加仍然为0.
△x无限接近于0,但不可能是最小的正实数,因为没有最小的正实数(实数0的下一个实数是什么?没有。假设0的下一个实数是a,我们永远可以找到a/2比0大,比a小。)
现在都是用epsilon-delta语言来描述极限
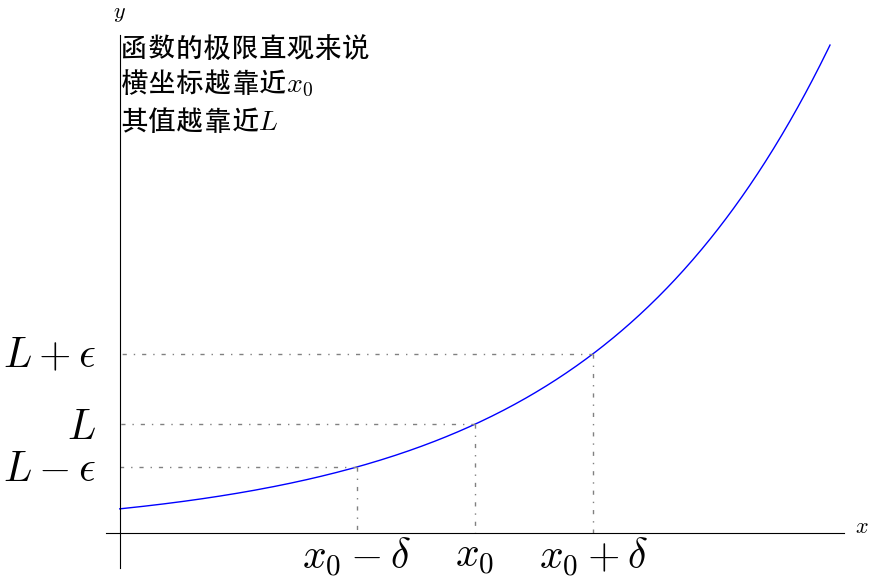
可以看到,极限的描述并没有用到什么无穷小量

导数的极限定义
在点x0的去心邻域内,△x=x-x0,lim(x->x0),即lim(△x->0)。0<△x<delta是一个小范围中某个极小的差值或者说增量。
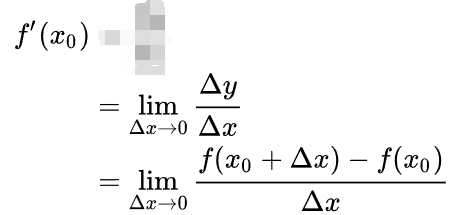
如此定义了导数,可以去定义微分

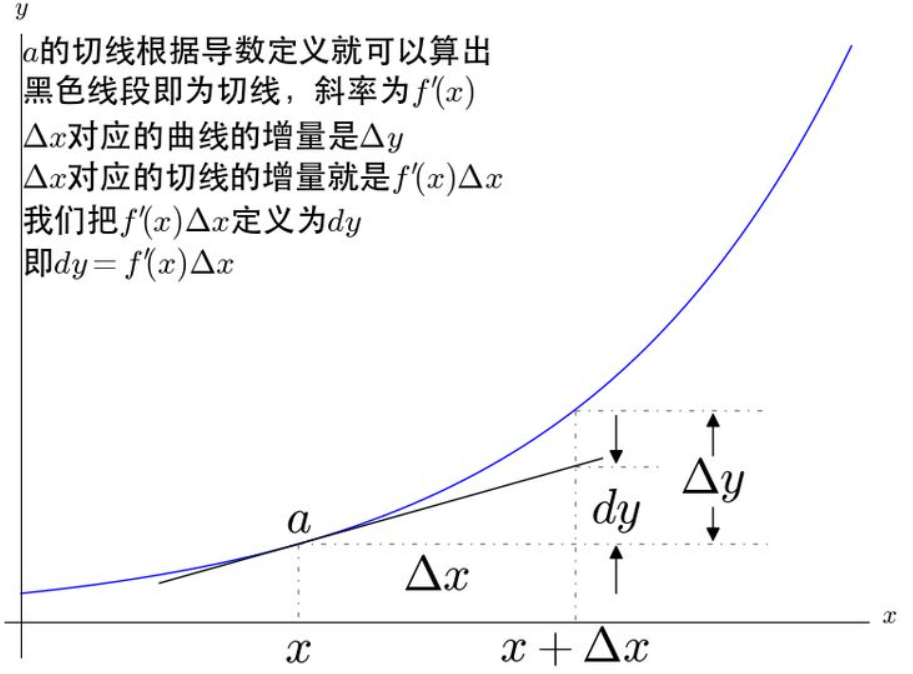
dy=f’(x)△x,这是dy的定义。我们是在用函数dy(几何上的切线)逼近原函数。
导数
- 导数是速度、是加速度、是变化率、是切线的斜率。
- 导数是用来找到“线性近似的数学工具”
- 导数是线性变换
导数是速度、是加速度、是变化率、是切线的斜率
物理中的变化率
一段时间的平均速度是位移/一段时间
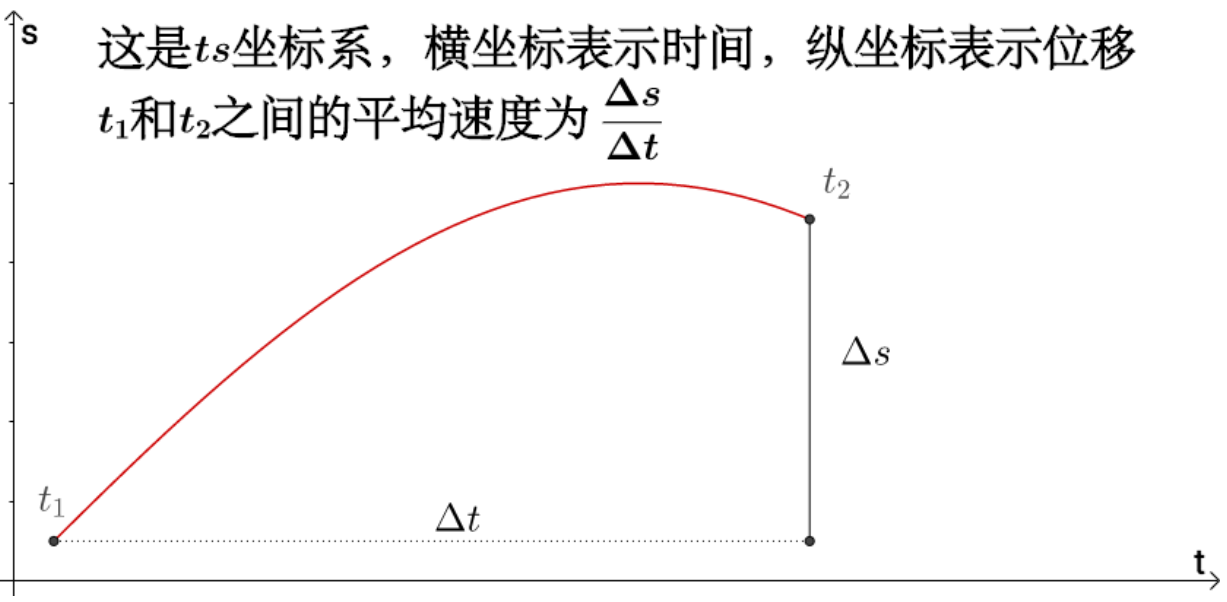
某一时间点的瞬时速度
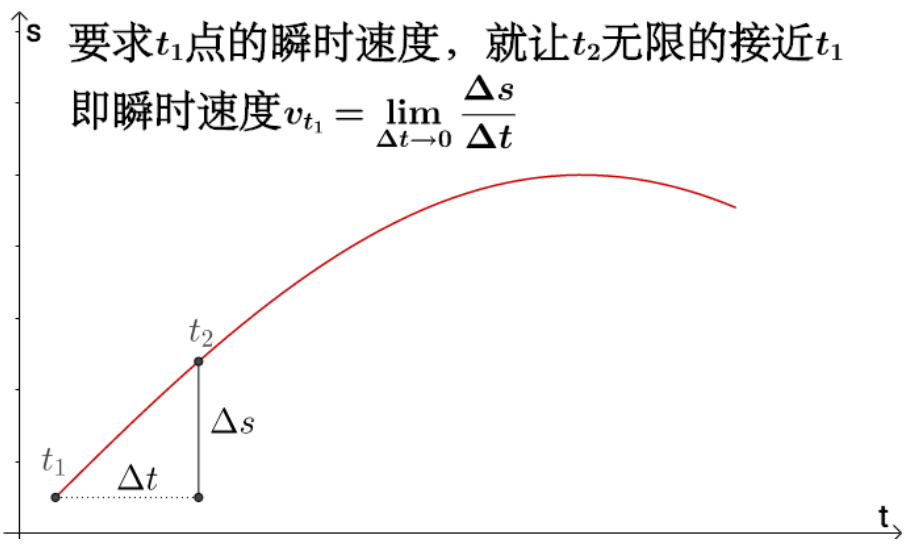
速度vt1就是t1点附近,位移增加值△s与时间增加值△t的比值,称这个比值为变化率,描述了t1点附近,时间增加值对位移增加值的影响程度。

同理,加速度就是速度对于时间的变化率。
几何的斜率
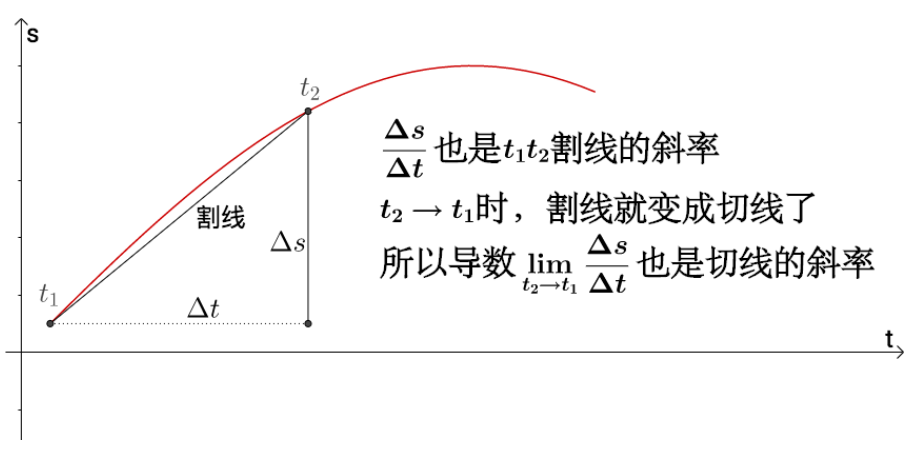
但是
在二元函数中,比如这样一个曲面上的一点α
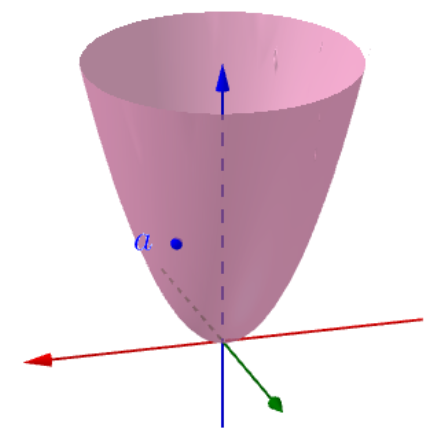
在曲面上可以做无数条过α点的曲线
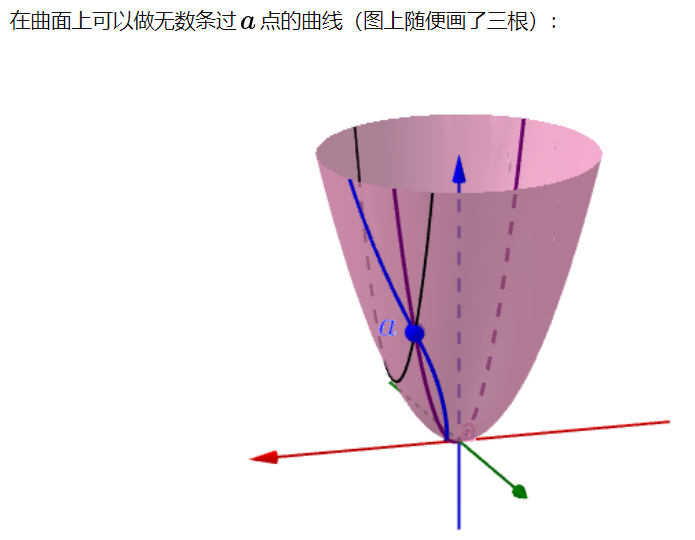
每根曲线都可能有切线,那么哪根切线的斜率是导数?
从一元函数到二元函数
所以我们认为,导数是某一点处,因变量增加值与自变量增加值的比值。导数是瞬时速度,是加速度,是切线的斜率。



