线性变换

线性代数

线性代数解决线性问题，把复杂问题线性化是别的学科的内容，比如《微积分》、《信号与系统》。

线性变换

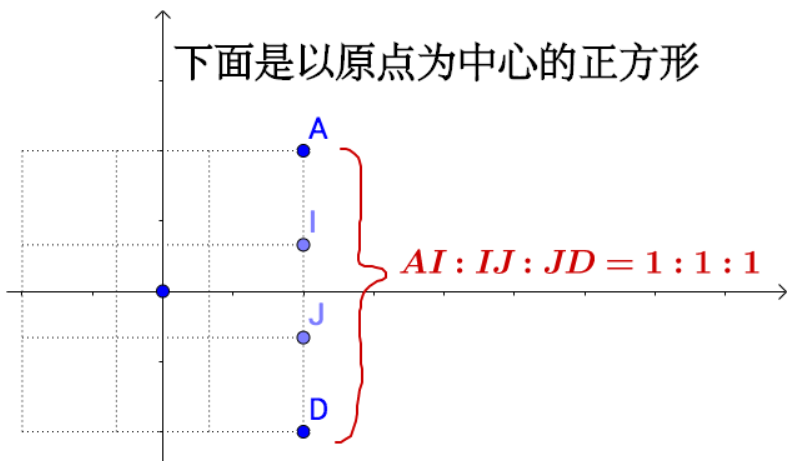
线性变换从几何直观有三个要点：

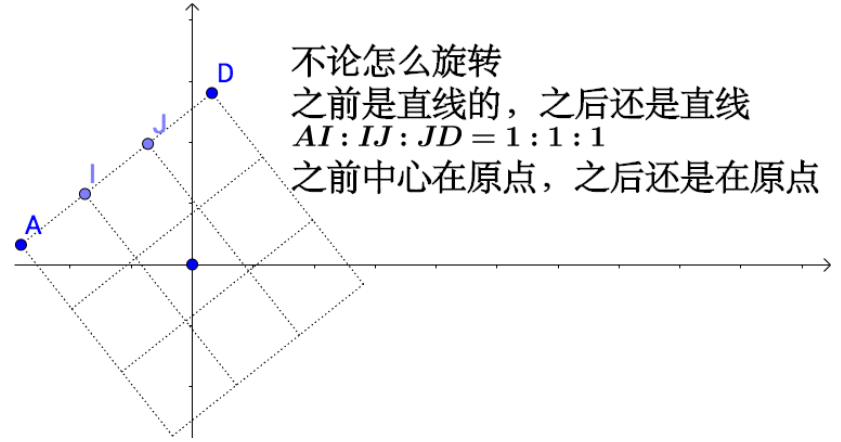
• 变换前是直线的，变换后依然是直线的
• 直线比例保持不变
• 变换前中心是原点的，变换后依然是原点

比如说旋转：

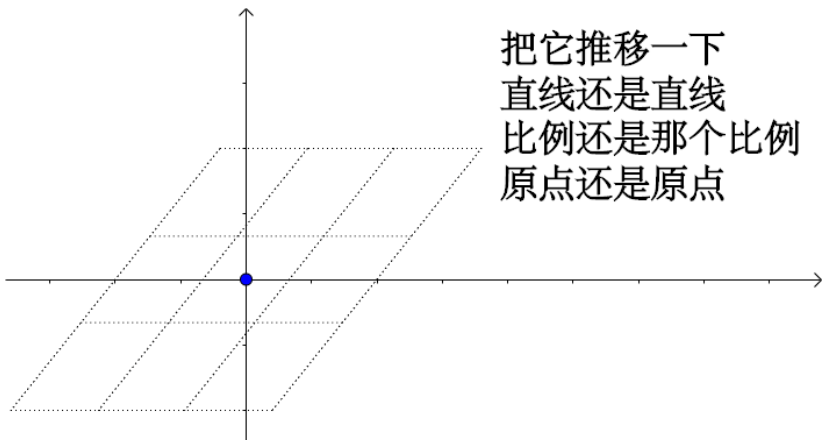
比如说推移：

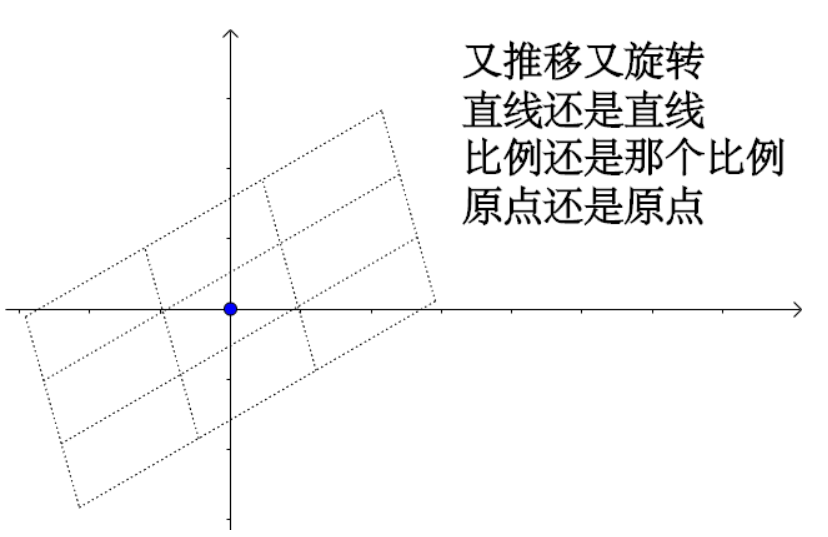
推移+旋转也是线性变换：

代数

简答讲一下旋转是怎么实现的，可以让我们进一步了解代数是怎么描述线性变换的。

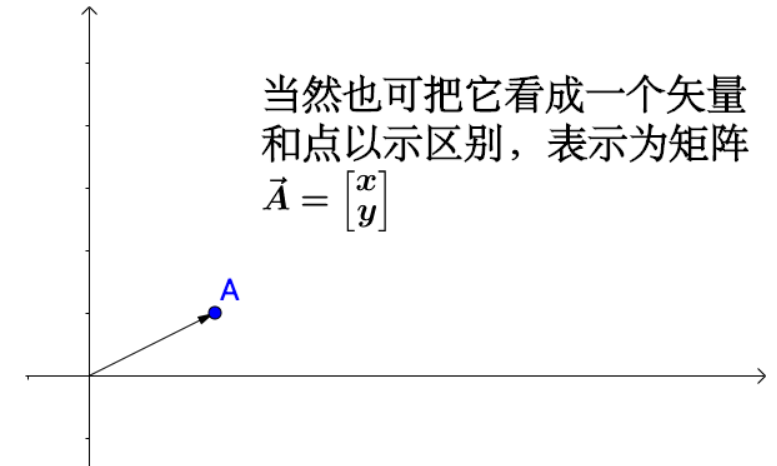
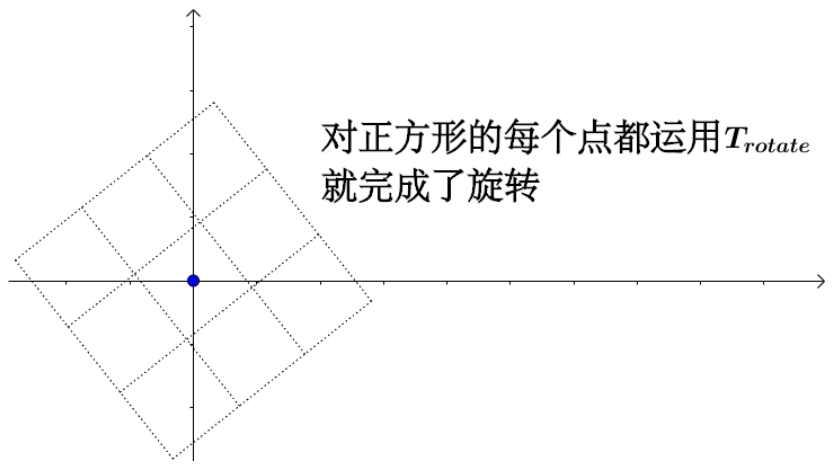
仿射变换

• 变换前是直线的，变换后依然是直线
• 直线比例保持不变

少了原点保持不变这一条。

比如平移：

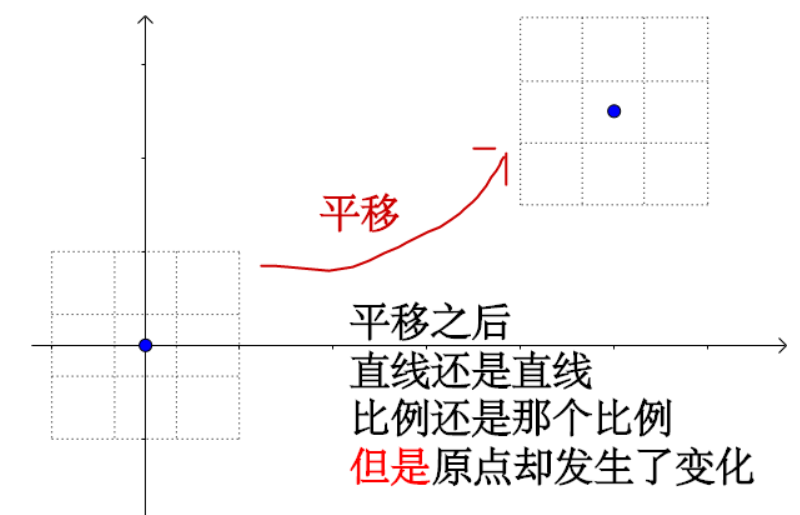
因此，平移不再是线性变化了，而是仿射变化

代数

线性变换是通过矩阵乘法来实现的，仿射变换不能光通过矩阵乘法来实现，还得有加法。

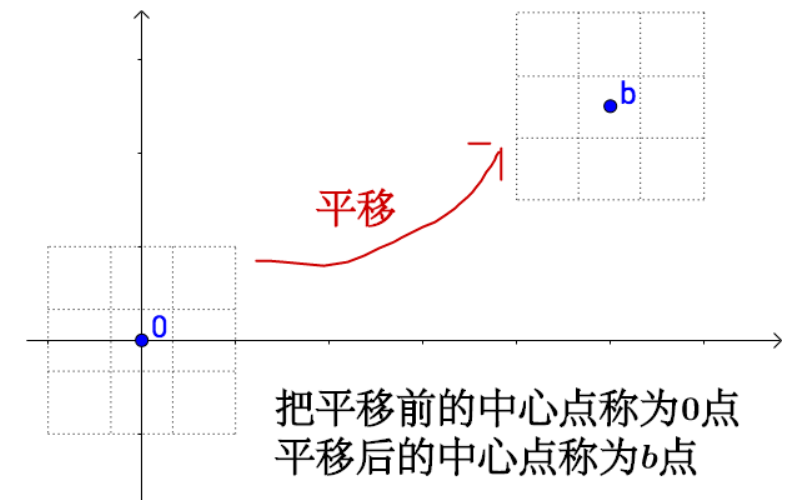
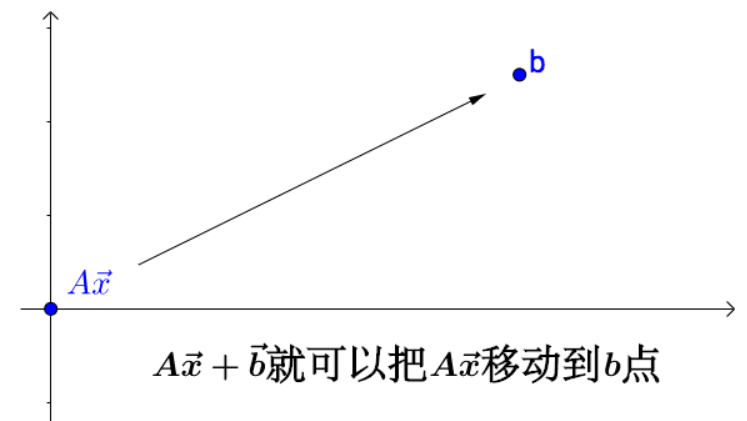
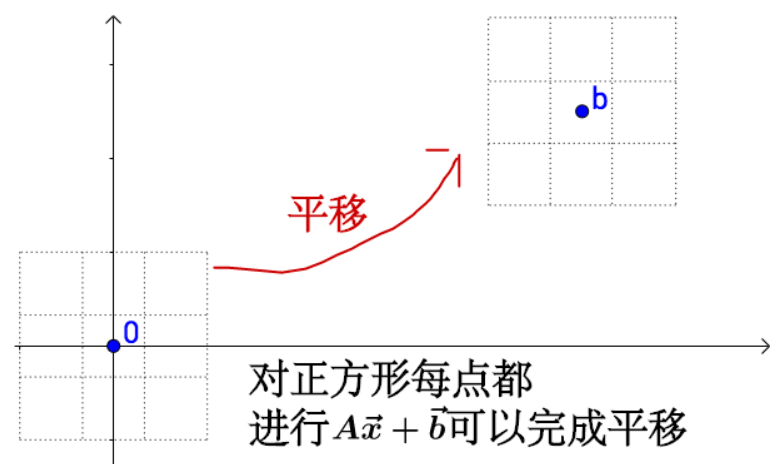
通过矩阵乘法来完成仿射