勾股定理
参考李永乐的视频
勾股定理
直角三角形的两条直角边的平方和等于斜边的平方
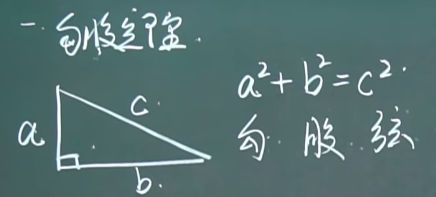
在中国,《周髀算经》给出了结论。三国时期吴国的赵爽在《周髀算经注》中给出了证明。
在古希腊,毕达哥拉斯提出了这个定理,但是证明失传了。欧几里得在《几何原本》中给出了证明,现在所学的几何内容与《几何原本》几乎一样。
三国时期吴国赵爽的证明
勾股圆方图:勾股各自乘,并之,为弦实,开方除之为弦。
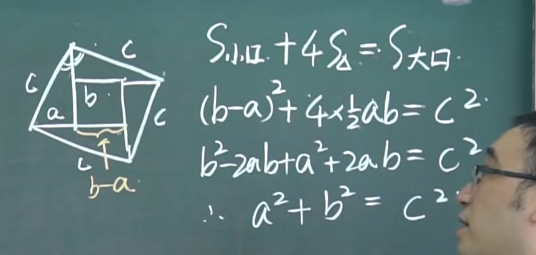
爱因斯坦十一岁时的证明
一个直角三角线,可以分割成2个与原直角三角形相似的直角三角形。
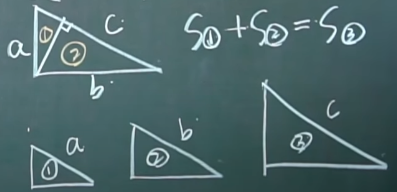
相似图形的面积之比等于边长的平方比
故S1+S2=S3即a^2+b^2=c^2
拓展
勾股定理将几何和代数联系在一起。
1
几何问题:直角三角形的三条边的边长都是正整数,能画出多少种?
等价于代数问题:满足a^2+b^2=c^2的正整数组(a,b,c)有多少组呢?
答:无穷组,因为(3n)^2 + (4n)^2 = (5n)^2
2
那符合上述条件的互素正整数数组有多少组?
【To Do】x^2+y^2=z^2的正整数解通式:x=2mn,y=m^2-n^2,z=m^2+n^2,m>n>0,mn互素且一奇一偶。
公元两百多年的代数之父丢番图
曾经写过一本书叫做《算术》,一个正整数的平方可否由另外两个正整数的平方和表示。
拓展指数——折磨数学家将近400年的费马大定理
1621年法国巴黎有一位20岁的律师买了一本《算术》看。突发奇想,写下一个整数的三次方不能拆分成两个整数的三次方和,一个整数的四次方不能拆分成两个整数的四次方和,以此类推,地方太小,证明过程我就不写了。
欧拉只证明了费马的前两句话是对的。1995年数学家怀尔斯给出了全部证明。
拓展项数——某点到原点的距离
三元组可以求二维直角坐标系中某点到原点的距离,四元组可以求三维直角坐标系中某点到原点的距离。
放宽等式的右边为一个整数——四平方和定理
任意的一个正整数都可以写成不超过四个正整数的平方和
丢番图一笔带过没给证明;费马说地方太小证明写不了;欧拉的学生拉格朗日用欧拉的四平方恒等式在1770年证明了四平方和定理,因此四平方和定理也叫作拉格朗日四平方定理;三年后欧拉也独立给出了证明。
一个正整数用正整数的更高次方的和来表示需要多少个——华林问题
1770年,英国数学家华林提出猜想,存在一个正整数g(k)(k表示k次方,g(k)是关于k的函数,如g(2)=4)使得每个正整数可以表示为至多g(k)个k次方数之和。
1909年,希尔伯特证明了华林猜想是正确的,但仅仅证明了存在g(k)。1909年证明了g(3)=9,1986年g(4)=19,1964年我国数学家陈景润证明了g(5)=37,那年陈景润31岁。
欧拉的小儿子给出了一个经验公式 g(k)=2^k + [(3/2)^k] - 2(中括号表示向下取整)。人们通过计算机验证,发现大概在1亿以下都是正确的。目前人们还不知道为啥它长这样,也困扰数学家几百年了。
给四平方和的每个项加一个系数,还能表示所有的正整数呢?
1916年印度神童拉马努金宣城他找到了所有的系数组合,只有这55组系数的平方数才能表示所有的正整数。其人自学成才,本职会计,33岁因病早逝,一生发现了3900多条数学公式和命题。
1993年英国数学家康威证明,康威发现拉姆努金给出的55组系数里,除了1、2、5、5不对,其他的54组都对,而且只有这54组。康威的这个证明叫15定理,因为他发现,所有系数的组合你任选一种,只要这个多项式能表示1-15之间的所有数,它就能表示所有的正整数。



