圆
参考妈咪说、李永乐的视频
无论圆的直径是多长,圆的周长比直径似乎都是一个定值,称其为圆周率π
圆面积
先把一个圆平均分成若干份,然后将其拼成近似的长方形,最后根据长方形与圆的关系推导出圆的面积公式为πr^2
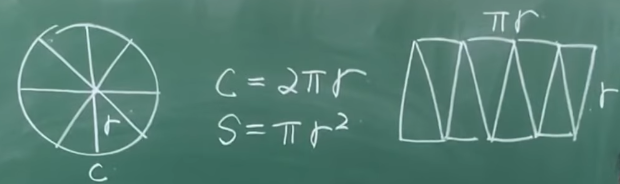
角度
两条直线的夹角,有大有小,用角度来衡量夹角大小。
设定全角为360°,全角的1/360为1°,1°的1/60是1‘,1’的1/60是1’‘。
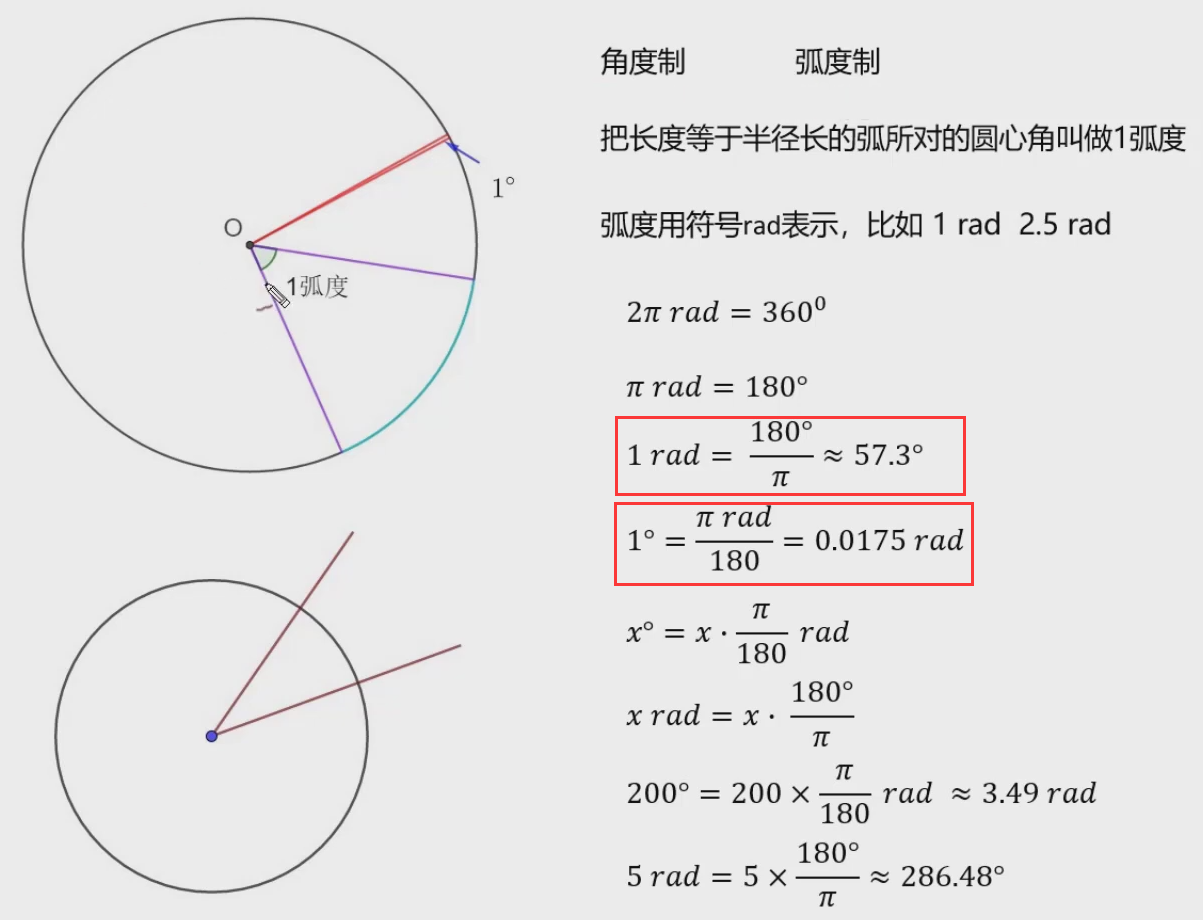
弧度
欧拉,把长度等于半径长的弧所对的圆心角称为1弧度。
sin,cos
从某个角度推一个箱子,力可以被分解为水平和垂直两个方向,其数值符合直角三角形的勾股数。直观感觉:sin,cos是用来分解力的工具。sin公式告诉你水平方向的分力与合力的比值,cos告诉你竖直方向的分力与合力的比值。
希望你看到公式能立刻想到
sinθ 是y方向的分解作用,5sinθ表示将合力5分解到y方向
cosθ 是x方向的分解作用,5cosθ表示将合力5分解到x方向
tanθ=sinθ/cosθ,是y方向分力与x方向分力的比值
和差角公式
巧妙的证明一
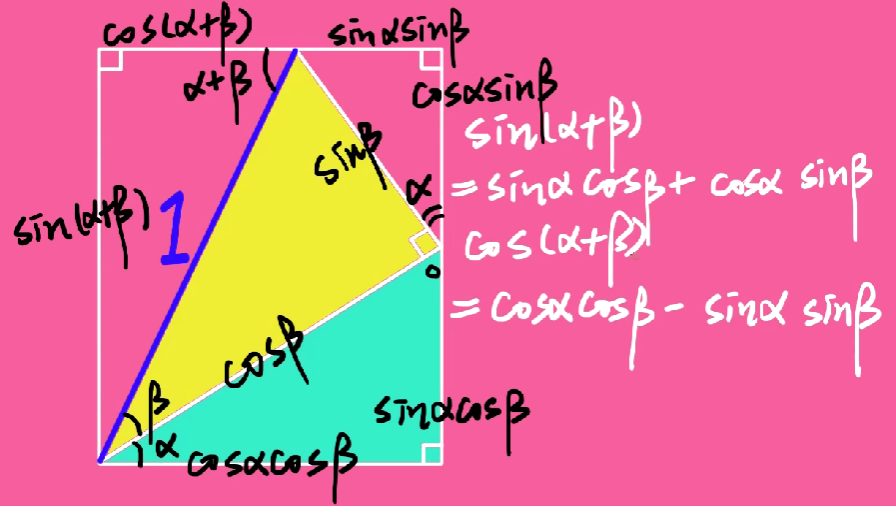
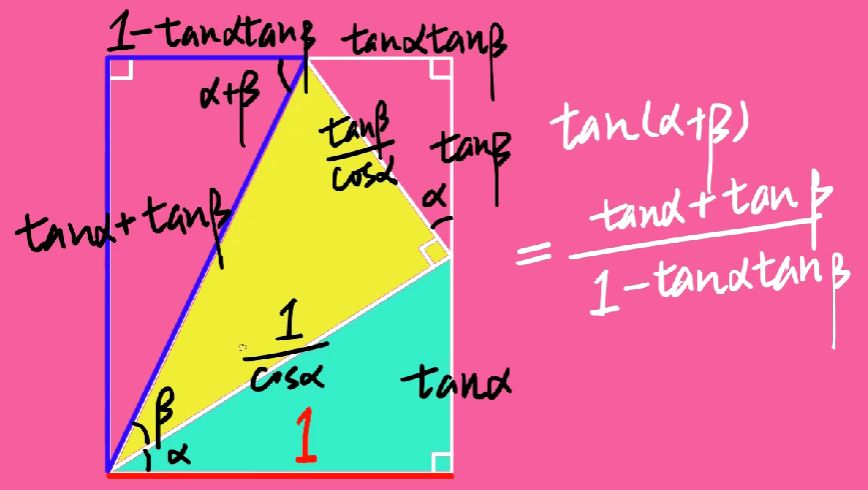
严谨的证明二
首先给出余弦定律
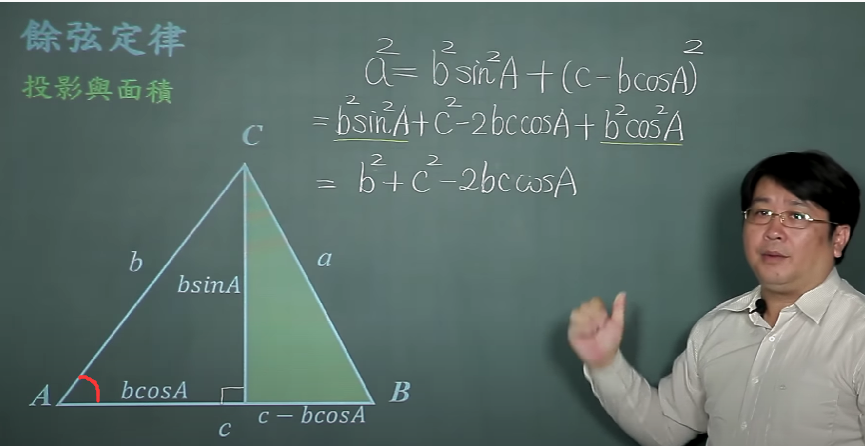
通过边长的两种求法,得出cos(α-β)
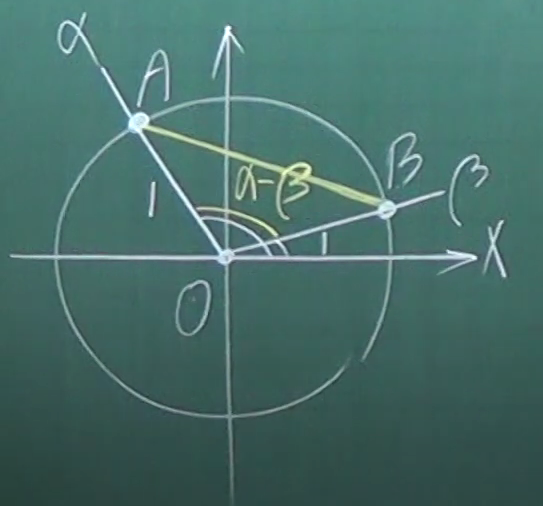
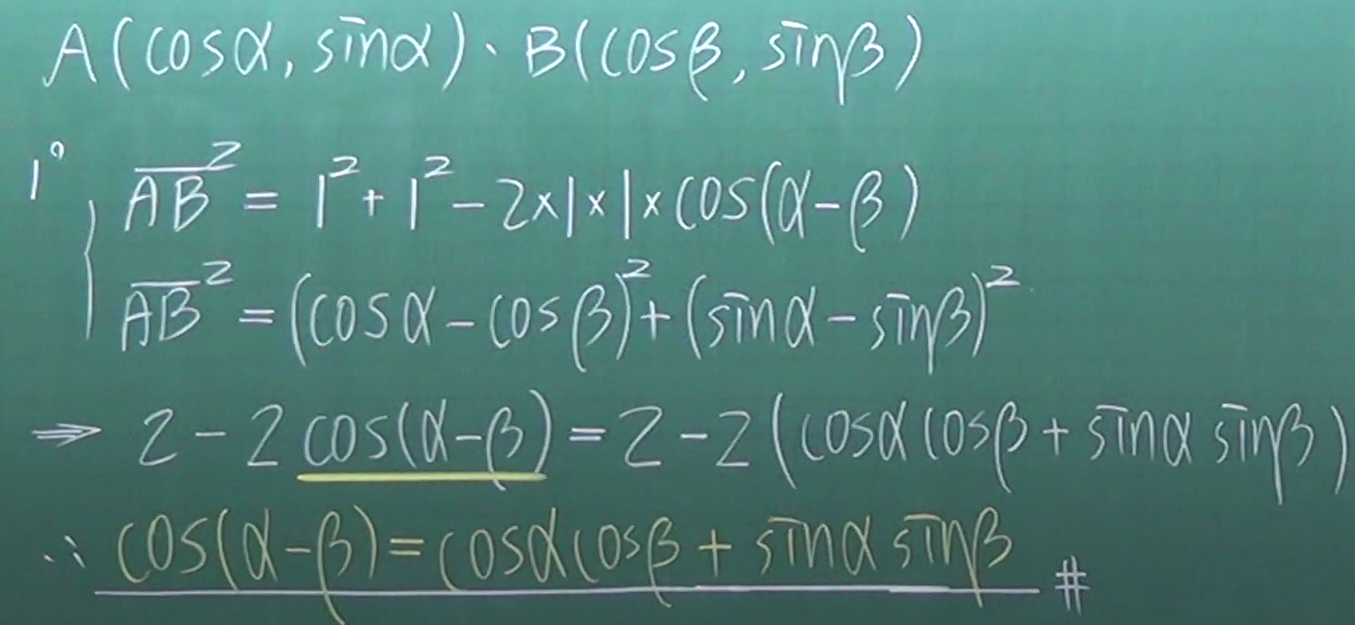
我们可以观察到cos(-α)=cosα,sin(-α)=-sinα
故cos(α+β)=cos(α-(-β))=cosαsinα-sinαsinβ
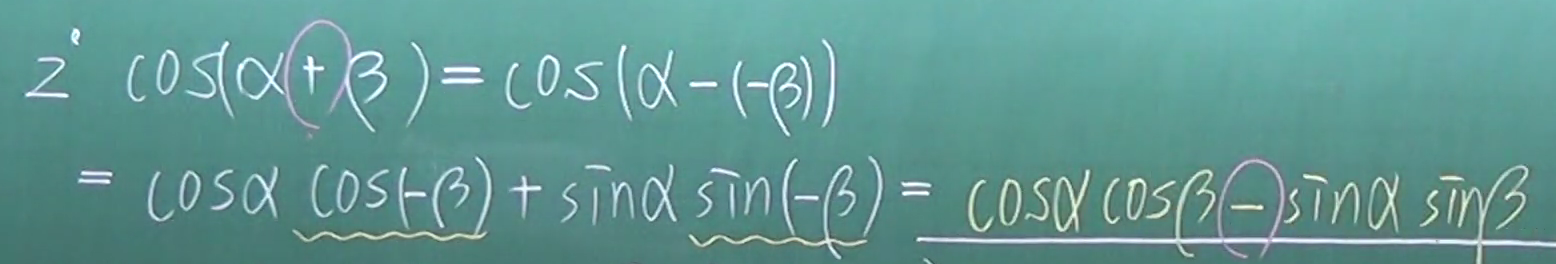
我们可以观察到sinα=cos(π/2 - α)
故sin(α+β)=cos(π/2-(α+β))=cos((π/2-α)-β)=cos(π/2-α)cosβ+sin(π/2-α)sinβ=sinαcosβ+cosαsinβ
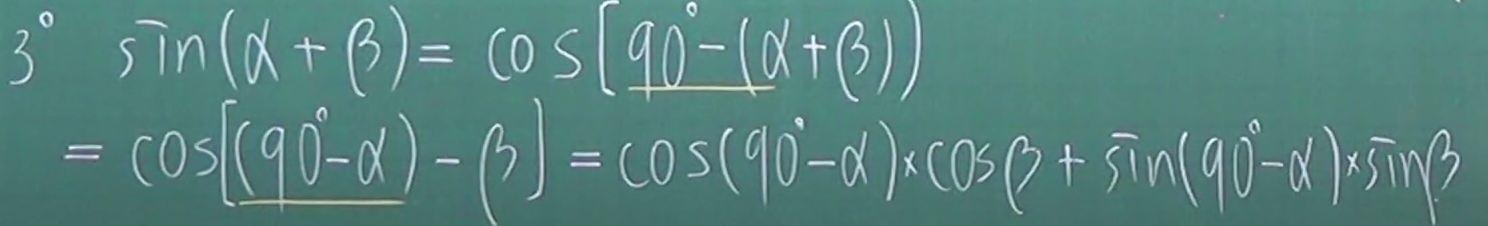
sin(α-β)=sin(α-(-β))=sinαcos(-β)+cosαsin(-β)=sinαcosβ-cosαsinβ
圆周率
古代方法-几何逼近
阿基米德-周长夹逼
第一个有严谨计算过程记录的圆周率算法,由公元前250年古希腊的阿基米德发明:内切正多边形与外切正多边形夹逼圆的周长。阿基米德一共计算到正96边形,得到223/71>π>22/7。
刘徽-面积夹逼
公元263年左右,三国时期魏国的数学家刘徽使用割圆术:用正多边形的面积夹逼
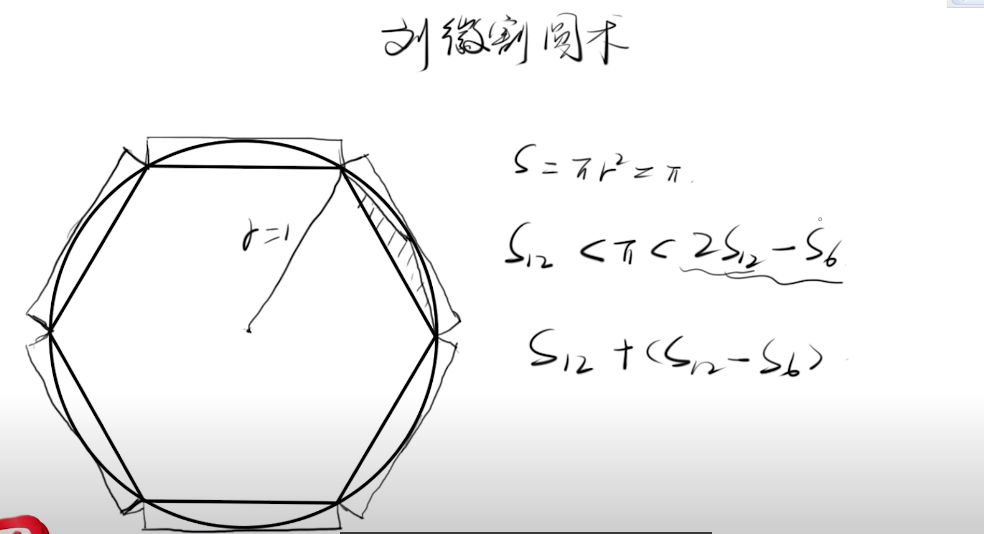
现代方法
法国数学家韦达,提出了第一个π的无穷项公式
园的内切正多边形的面积

韦达π公式
圆的半径为1,内切正四边形面积/圆面积=2/π。
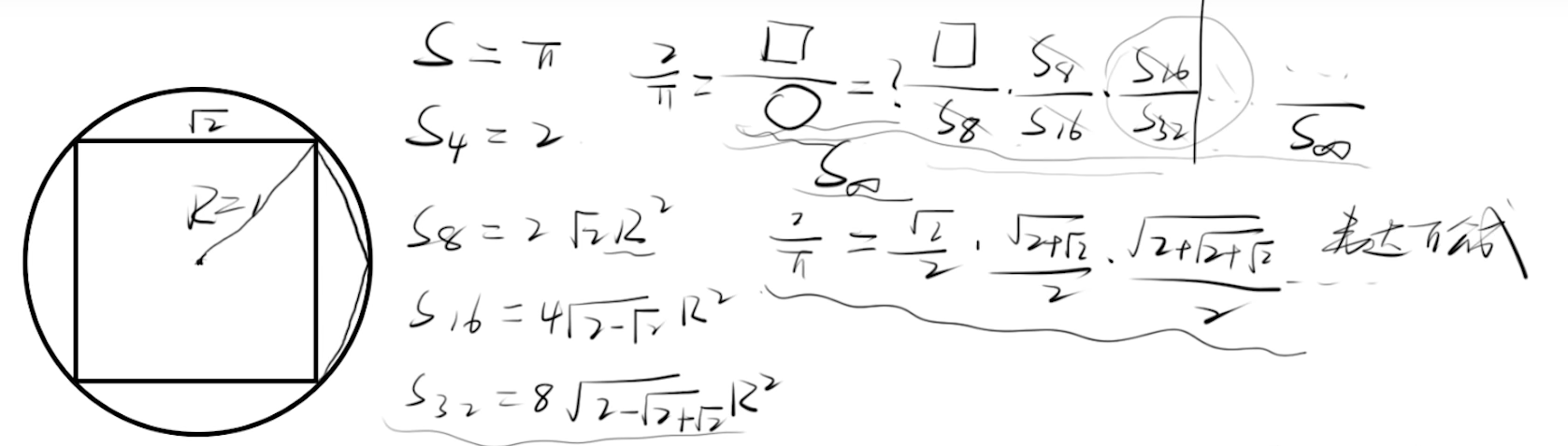
沃利斯乘积公式
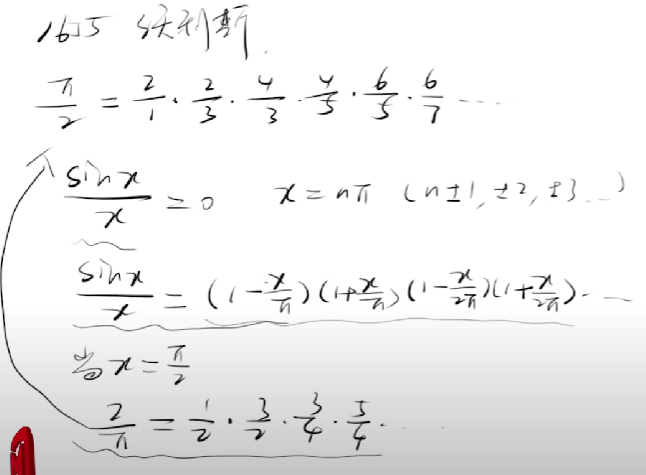
蒙特卡洛算法:冯诺依曼和乌拉姆发明,因为吾拉姆的叔叔经常去蒙特卡罗赌场,蒙特卡罗是以赌场闻名于世的地方,赌场与概率有关,就叫做蒙特卡罗算法了。
欧拉-巴塞尔问题
π的莱布尼兹公式
高斯-梅钦类公式
拉马努金
收敛速度更快
楚德诺夫斯基兄弟
蒙特卡洛方法
落点在圆中的概率=圆面积/正方形比
布丰的针




