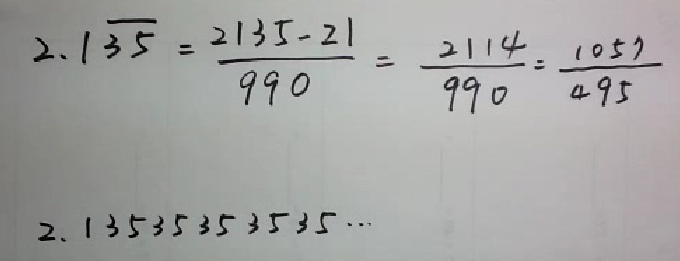[高等微積分] 第1講、數學的本質 - YouTube 数学的本质：公理->定理->定理->…->定理。公理是这个世界的真理，是人所观察到的，这个世界中不变的东西——律。

第一次数学危机

毕达哥拉斯是希腊的主要数学家

他的主要观点是万物皆数-有理数(rational翻译错误，应为可比，以后都称有理数为可比数，无理数为不可比数)

可比数可以表示成整数之比，分为三类

无限循环小数转换成分数

分母：小数点后循环部分有几位，分母开头就有几个9，小数点后不循环部分有几位，分母结尾就有几个0。

分子：去掉小数点后的整数，减去去除循环部分的整数。

令x=不循环小数，根据小数的不循环部分(假设1位)和循环部分(假设2位)，得到等式如1000x-10x=整数相减，去掉循环部分，最终得到如x=整数/990的分数。

希帕索斯：如果有一个直角三角形，x=1，y=1，z=根号2，根号2是个啥？毕达哥拉斯把希帕索斯绑到大石头上扔到爱琴海里了。

实际上，实数=可比数+不可比数

第二次数学危机

其实在古希腊时代就已经有了，古希腊有一个数学家叫芝诺，他研究了很多的悖论。

阿基里斯A与乌龟B相距L，阿基里斯从a1跑到乌龟原来的位置a2，乌龟向前走一段到了a3；阿基里斯从a2跑到a3，乌龟又往前走了一段到a4，所以阿基里斯永远追不上乌龟。

设阿基里斯的速度为VA=2VB。则阿基里斯跑的路程和花费的时间为

$S_A=L+{1\over2}L+{1\over4}L+{1\over8}L+...=2L-{1\over2^n}L$ $t_A=t+{1\over2}t+{1\over4}t+{1\over8}t+...=2t-{1\over2^n}t$

n->∞的时候，两个公式的最后一项无穷小。

芝诺的问题在于，它把一个有限的长度分割成了无限多份，但是这些份加起来并不是一个无穷长的时间和路程。

各自独立发明了微积分

微积分中有一个重要的概念，是导数

假如有一个function y=f(x)，在二维坐标轴上表示为曲线，取点A和点B，这两个点就会有一个横坐标的差△x和纵坐标的差△y，如果△x->0，B点就会非常非常接近于A点，B点非常接近于A点的时候，△y/△x=f(x)在A点的导数。

人们通过导数以及微积分解决了很多数学和物理上的问题，所以人们觉得这是很正确的。直到有一天，英国的大主教提出了问题。

贝克莱：△x(无穷小)是否为0，若是，△x凭什么做分母，若不是，凭什么说B点与A点重合成一个点呢？所以微积分的基础是有问题的。

第二次数学危机持续了150年。直到像阿贝尔、柯西、康托尔等人对无穷小进行了严格的定义，从而使微积分具有了坚实的基础。

理发师：“我给且仅给自己不刮胡子的人刮胡子”。

那么理发师该不该给自己刮胡子呢？

如果他给自己刮胡子，他自己就刮胡子，他就不该给自己刮胡子，矛盾。

如果他不给自己刮胡子，他就应该给自己刮胡子，矛盾。

悖论就是怎么说都矛盾。

罗素为什么提出这么一个奇怪的问题呢？是要诘难德国数学家康托尔。

康托尔提出了集合理论，集合理论被认为是现代数学的基础。用集合去解释现代数学中的一些问题，这个理论后来被人们称为人类纯智力活动的最高成就。

集合有瑕疵。他不说，罗素就问他。

集合有3个特点

美女不能构成集合，因为美女，有人觉得美，有人觉得不美，这是不确定的，不符合集合的确定性。

定义A={x|x∉A}

若A∈A=>A∉A

若A∉A=>A∈A

这件事情到目前为止，还没有被完美地解决，所以这件事被称为第三次数学危机。

康托尔一次一次经受着罗素的诘难，他又解释不了，他就疯掉了，最后死在自己工作的哈勒大学精神病院里面。