参考：

Youtube->万门好课——《五分钟数学漫谈》。

知乎——胖三sir的专栏《初中数学那些事》

CSDN——(44条消息) 希尔伯特及其《几何学基础》电子版（英文PDF），_袁萌专栏-CSDN博客

数学的开始

相传，古希腊数学家泰勒斯引入了划时代的几何证明思想。数学家们开始不再满足于知其然了，而致力于知其所以然。通过公理或已证明命题(定理)推理出新的定理，在各定理之间建立起了联系，使数学逐步形成了一个严密的体系。

物理和数学

物理的研究对象是真实世界中的东西或者说对象，研究其属性或行为。如一只猫的叫声，捕食；形状，颜色，长度，速度，重量等等。研究手段是简单化和理想化(如一个苹果，变成纸上的一个点)的真实对象——逻辑对象。逻辑对象有人为规定的一些属性。人的一切知识都是由已知的经验产生的。

数学研究逻辑世界中的东西，是物理学的研究手段，如符号，公理，推导规则，推论形成公理体系。逻辑世界是简单化和理想化后的真实世界。

几何一词的由来，目的和发展

几何：长宽几何？面积几何？

代数：以符号代数，求数。

英文Geometry一词,是从希腊语演变而来的,其原意是土地测量、后被我国明朝大学士徐光启翻译成”几何学”。依据大量实证研究,创造几何学的是埃及人,几何学因土地测量而产生。

几何是研究形的科学,以人的视觉思维为主导,培养人的观察能力、空间想象能力和洞察力。

几何的发展首先是欧几里得的欧氏几何,其次是19世纪上半叶,非欧几何的诞生,再次是射影几何的繁荣,最后是几何学的统一。

尺规作图

尺规作图是有2000多年历史的古老的数学游戏，在被古希腊人发明之后在全世界影响巨大，成为了科学与数学思想的源泉。

阿基里德：

给我一根杠杆，我能撬动地球。
浮力定律的发现者。
采用前人尺规作图的思想和朴素的极限思想，证明了球表面积公式和球体积公式。

牛顿：

牛顿三定律
万有引力定律
微积分的发明人
《自然哲学的数学原理》，其创作灵感得益于之前的尺规作图训练，这本书中的很多命题都是由几何作图的方式证明的，与我们现在能看到的教科书上的处理方式有所不同。

高斯：

十九岁，探索出了正十七边形的尺规作图方法尺规作图正十七边形——高斯 - 知乎 (zhihu.com)
贡献繁多

与尺规作图有关联的问题和数学分支简略示意图

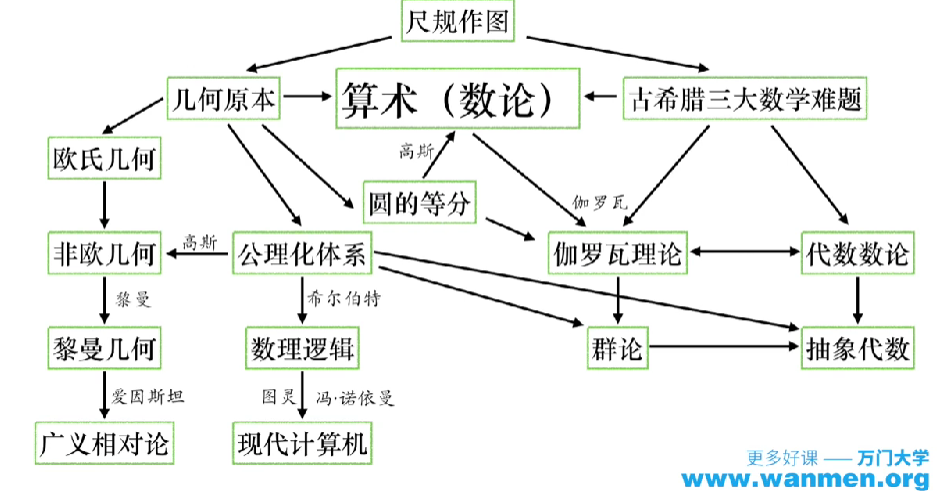
几何原本简介

13卷，700多页，是对古希腊数学学派2个多世纪间研究的数学问题的收集、整理与完善。

内容不只涉及有关尺规作图的几何问题，还有很多算术问题，如素数无穷多的证明在书的第九章。故也称《原本》。

内容安排：

采用公理化体系

一切开始于23条定义+5条公设+5条公理，推出了465个命题

ps：欧几里德是这样区分公理与公设的：
第一,公理适合于一切科学,而公设是几何所特有的；
第二,公理是无需证明的真理,公设没有公理那样显然,但也是不加证明而承认其真实性的.
时至今日,人们已不在区分公理与公设了,都用公理一词来表明.

公理化体系

公理要尽可能的少，而且要直观简洁
从不同的公理推理出来的同一个命题不能相互矛盾——一致
公理不能由其它公理推导出来，不然该公理毫无意义——独立
整个公理体系中的每个命题都能够由这些公理推理得到——完备

五大公理(common notions/axioms)

等于同量的量彼此相等。Things which are equal to the same thing are also equal to one another
等量加等量，其和仍相等。If equals be added to equals, the wholes are equal
等量减等量，其差仍相等。 If equals be subtracted from equals, the remainders are equal
彼此能重合的物体是全等的。 Things which coincide with one another are equal to one another
整体大于部分之和。The whole is greater than the part

五大公设

两点可以连成一条直线
线段可以任意延长
绘定点o，及线段长r，可以以o为圆心，半径为r，可作一圆
凡直角皆相等 That all right angles are equal to one another
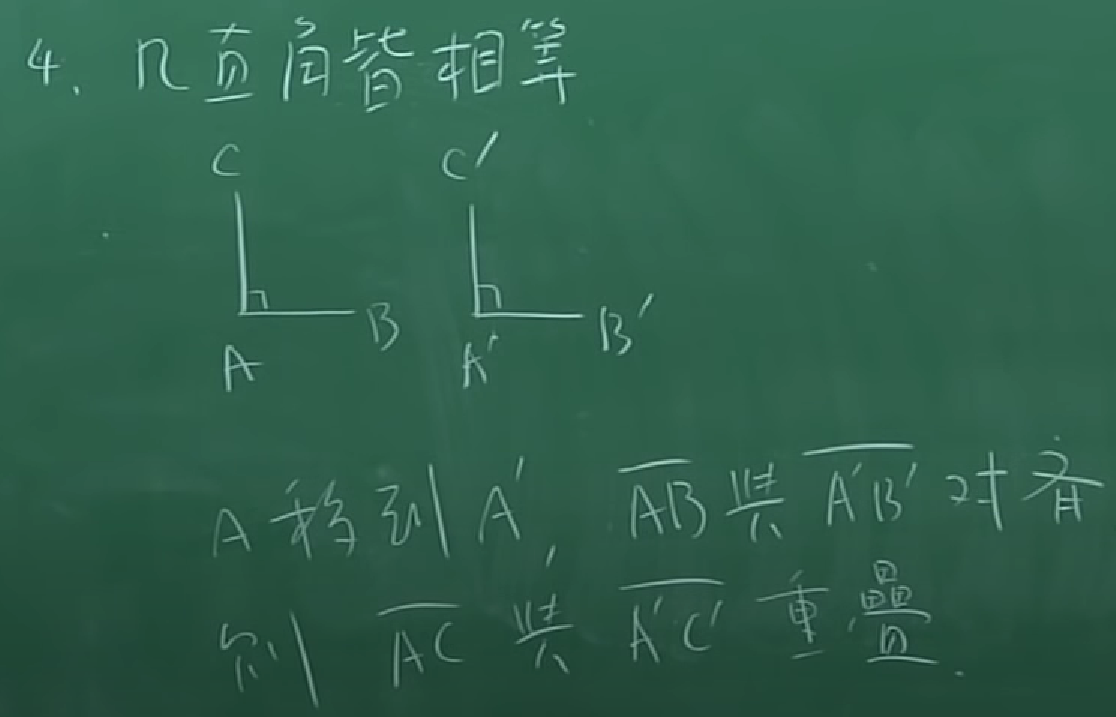
平行公理同平面内一条直线和另外两条直线相交，若在某一侧的两个内角的和小于二直角的和，则这二直线经无限延长后在这一侧相交 That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that that side on which are the angles less than the two right angles

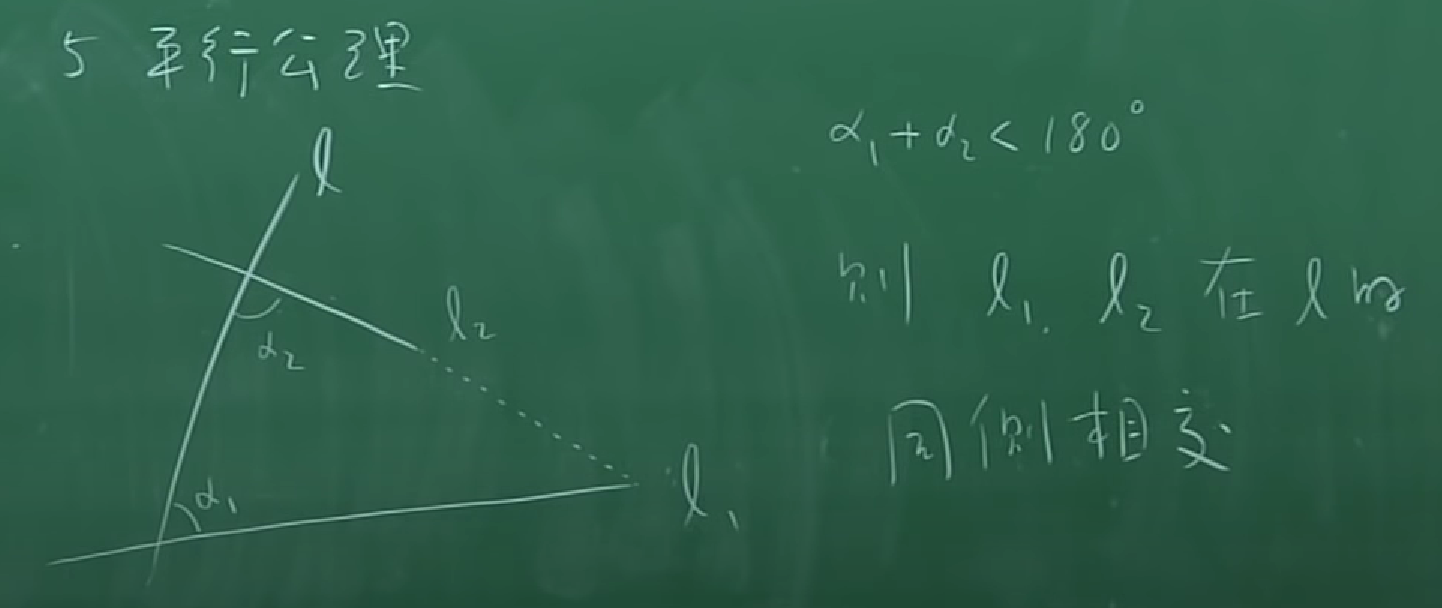
等价命题(从平行公设出发可以推出这个命题，从这个命题出发可以推出平行公设)：

过直线外一点可做唯一一条平行直线

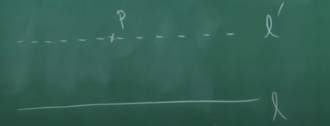
三角形内角和为180度

存在一对相似但不全等的三角形

若两条直线都平行于第三条，那么这两条直线也平行

等等等…

五大公设并不完备

比如，不能解释求线段AB的中点，分别以A和B为圆心，画两个圆，为什么两圆必然相交，交于两点？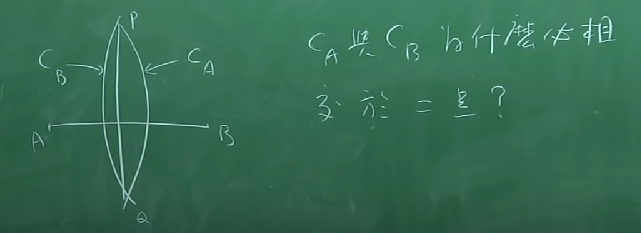

几何原本中的一些定义和缺陷

Health的13卷及其陕西科学技术出版社2003年的译本。

内容取自Heath写的《The thirteen books of Euclid’s Elements》，及其陕西科学技术出版社2003年的译本。

23条定义

几何原本的定义只是对一些基本概念的并不精确的描述，如果我们以苛刻的眼光来看，原本中的定义是不严格的。

Book1中的一些定义

点是没有部分的 A point is that which has no part //什么是部分?
线只有长度没有宽度 A line is breadthless length //什么是宽度和长度?
一线的两端是点 The extremities of a line are points
直线是它上面的点一样地平放着的线 A straight line is a line which lies evenly with the points on itself //什么是平放、均匀放置的点？如果点没有部分，线怎么会有长度？
面只有长度和宽度 A surface is that which has length and breadth only. //如果线没有宽短，面的宽是从哪里来的？
面的边缘是线 The extremities of a surface are lines
平面是它上面的直线一样地平放着的面 A plane surface is a surface which lies evenly with the straight lines on itself

等等……

Book XI(13卷)中的一些定义

体有长、宽和高 A solid is that which has length, breadth and depth
体的边界是面 An extremity of a solid is a surface

等等……

Book1 中定义了的概念

点、线、直线、面、平面

平面角、直角、钝角、锐角

圆、圆心、直径、半圆

三角形、等边三角形、等腰三角形

四边形、正方形、长方形、菱形

平行直线

尺规作图游戏规则

几点误区

直尺上有刻度
作图时，可以用圆规比好长度再去做另外一点
可以借助三角板作垂线
可以借助三角板加直尺做平行线

游戏规则-五大公设(postulates-假设)中的前三条

两点可以连成一条直线 To draw a straight line from any point to any point
一条有限直线可以继续延长 to produce a straight line continuously in a straight line
以任一点为心及任意距离可以画圆 To describe a circle with any centre and distance

简单的讲：过任意两点可以做唯一的直线，以任意两点可以做唯一的圆

几何原本第一卷中的命题

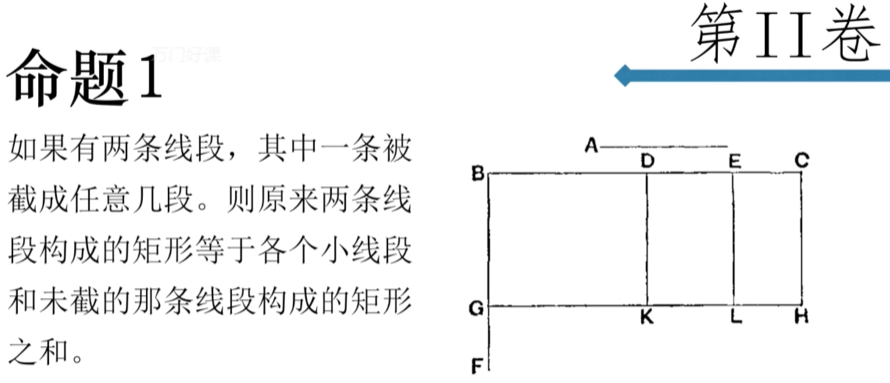
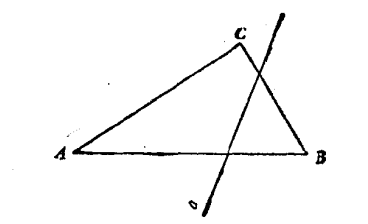
命题1

在一个已知有限直线上作一个等边三角形

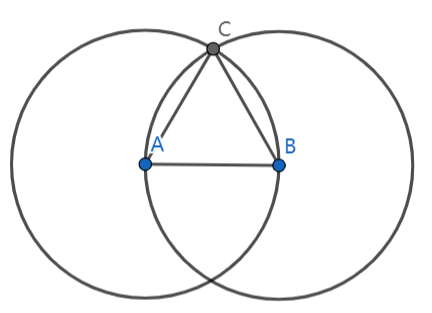
以A为圆心，AB为半径作圆A [公设3]

以B为圆心，BA为半径作圆B [公设3]

两圆交于点C //几何原本的公理体系实际上并不完善

连接AC与BC [公设1]

AC等于AB，并且BC等于BA [定义15]

AB等于BA

所以AC等于BC [公理1]

ABC为等边三角形 [定义20]

命题2

由一已知点，作一线段等于已知线段

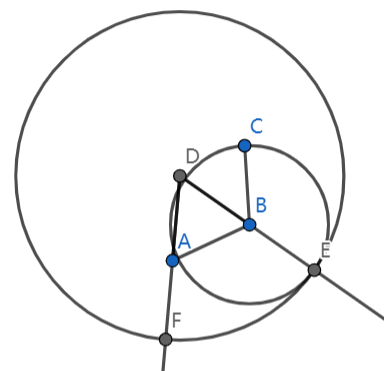
连接AB并作等边三角形ABD [公设1][命题1]

以B为圆心，BC为半径作圆B [公设3]

延长DB和DA [公设2]

DB交圆于E

以D为圆心，DE为半径作圆D [公设3]

DA交圆D于F

BC等于BE, DE等于DF [定义15]

DA等于DB [定义20]

AF等于BE, 从而等于BC [公理3][公理1]

AF为所求

命题3

已知两条不相等的线段，试由大的上边截取一条线段使它等于另外一条

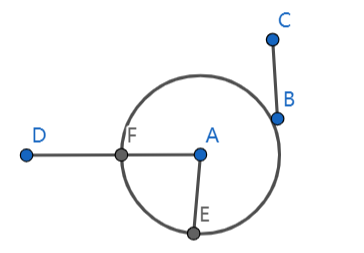
从A出发画出与BC相等的线段AE [命题2]

以A为圆心，AE为半径，画圆 [公设3]

圆A于AD交于点F

AF等于AE [定义15]

AF等于BC [公理1]

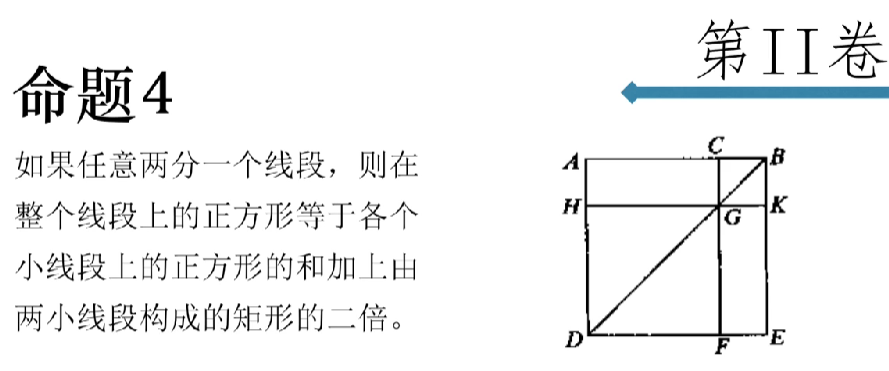
命题4

若两个三角形的两边和夹角分别相等，则这两个三角形全等。江湖人称边角边或SAS(side angle side)

移动相等角的顶点，使角重合，由于两边相等，所以两边也重合，由于过两点只能做唯一一条直线，所以相等角的对边相等。另外两角的边都重合，故另外两角也相等。

平移、旋转、镜面对称——保距变换

距离、角度、面积、体积等量在这些变换下保持不变。

保持距离的变换，称为保距变换，只有平移、旋转和镜面对称

命题4能推出的命题

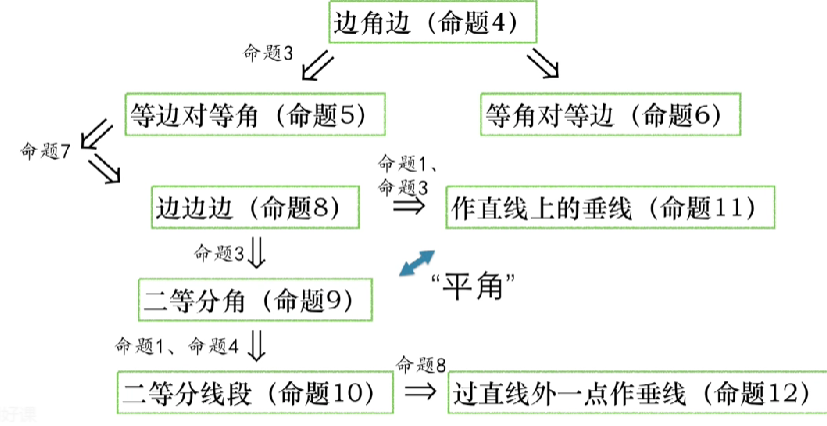
第一卷命题内容梗概

第一卷的高潮，命题47

几何原本中对勾股定理的证明

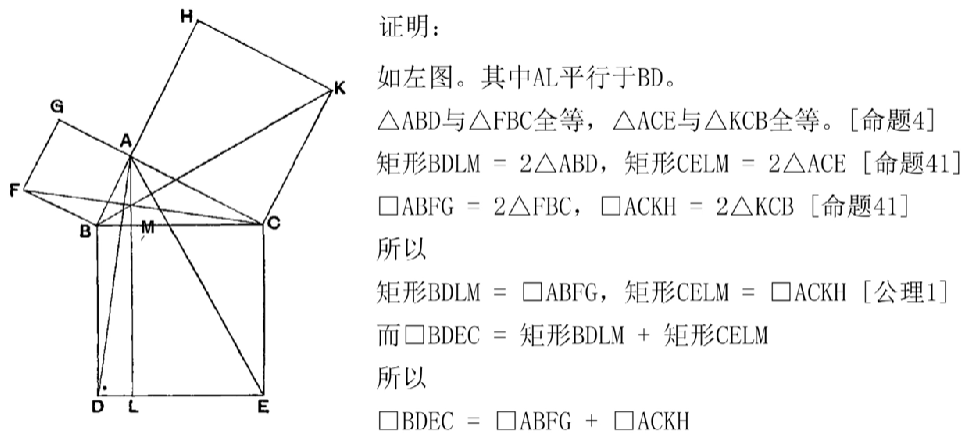
几何原本第二卷中的命题

第二卷命题内容梗概

第二卷也被称为几何代数

定义

称两邻边夹直角的平行四边形为矩形 Any rectangular(矩形的) parallelogram(平行四边形) is said to be contained by the two straight lines containing the right angle
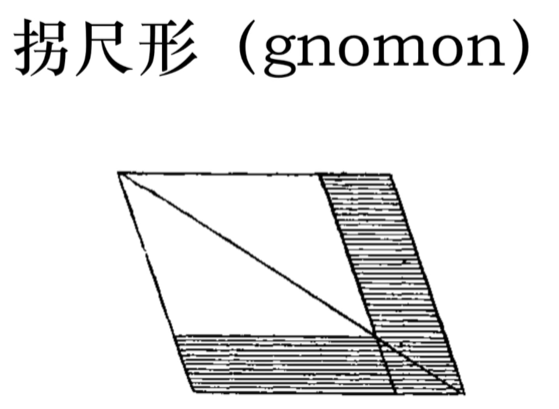
在任何平行四边形面片中，以此形的对角线为对角线的一个小平行四边形和两个相应的补形一起叫做拐尺形 And in any parallelogrammic area let anyone whatever of the parallelograms about its diameter(对角线) with the two complements(补形) be called a gnomon(拐尺形)

命题1

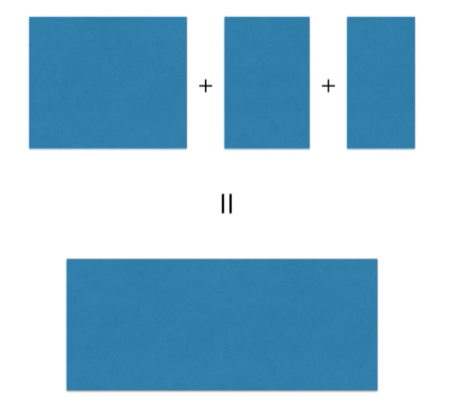
命题4

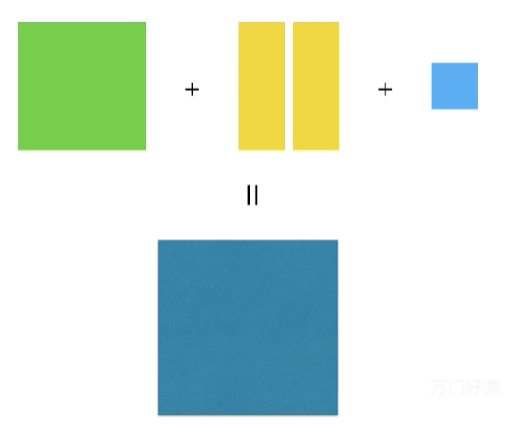
第二卷前10个命题的代数表达

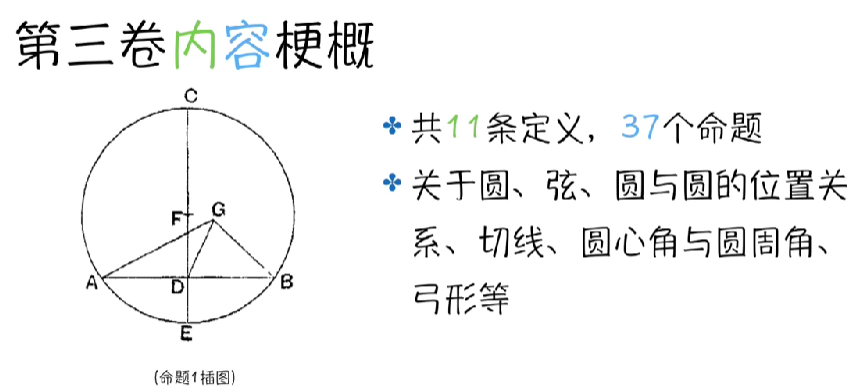
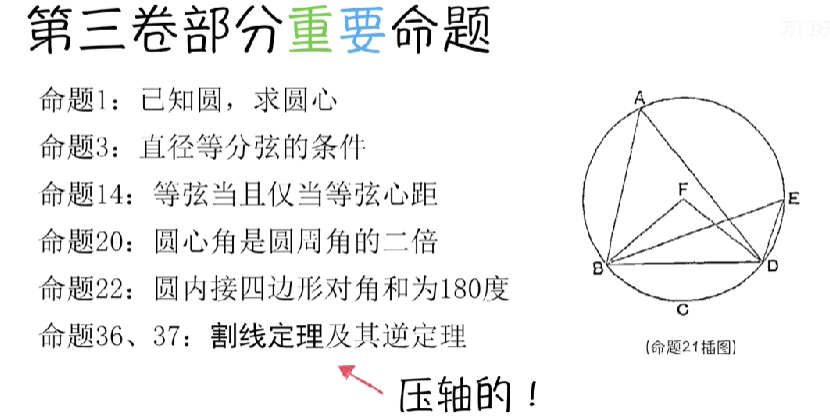
几何原本第三卷

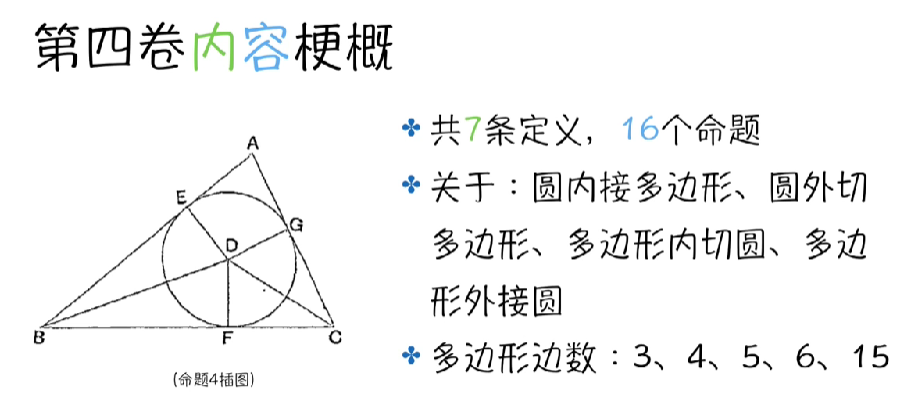
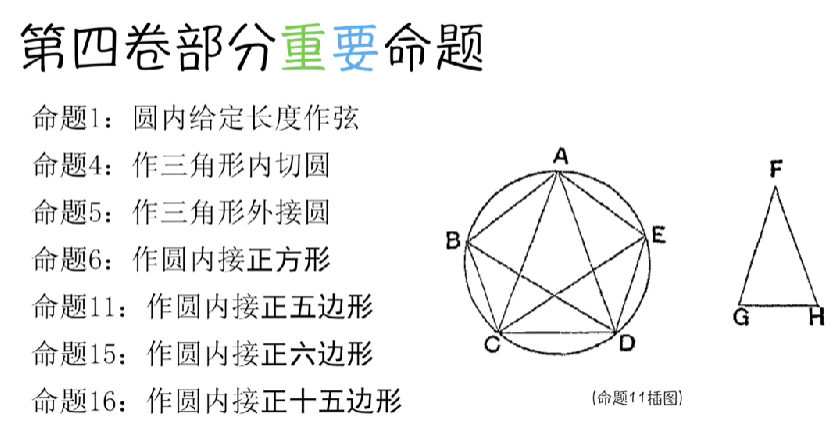
几何原本第四卷

几何原本第五卷：比例论

提出者：欧多克索斯(Rudoxus)，柏拉图的学生和好友

定义

当一个较小的量能量尽一个较大的量时，我们把较小量叫做较大量的一部分 A magnitude is a part of a magnitude，the less of the greater，when it measures the greater
当一个较大量能被一个较小量量尽时，我们把较大的量叫做较小的量的倍量 The greater is a multiple of the less when it is measure by the less
两个同类量彼此之间的一种大小关系叫做比 A ratio is a sort of relation in respect of size between two magnitudes of the same kind
把一个量几倍以后能大于另外一个量时，则说这两个量彼此之间有一个比 Magnitudes are said to have a ratio to one another which are capable，when multipled，of exceeding one another
有四个量，第一量比第二量与第三辆比第四量叫做有相同比，如果对第一与第三个量取任何同倍数，又对第二与第四个量取任何同倍数，而第一与第二量之间依次有大于、等于或小于的关系，那么第三与第四倍量之间便有相应的关系 Magnitudes are said to be in the same ratio，the first to the second and the third to the fourth，when，if any equimultiples whatever be taken of the first and third，and any equimultiples whatever of the second and the fourth，the former equimultiples alike exceed，are alike equal to，or alike fall short of the latter equimultiples respectively taken in corresponding order

几何原本第六卷

什么是定义？

亚里士多德

下定义不过是给个新名字，在给出定义的时候，必须使用已有明确意思的事物。
一个理论中最基本的那些东西，是无法定义和证明的。

对于几何中最基本的的点、线、面的概念，我们该怎么定义呢？这个问题困扰了世人很久，2000年后，希尔伯特横空出世。

无法定义的基本概念

两千年中，数学家们不断尝试给”点、线、面”一个严谨的定义，然而始终做不到，欧几里得的几何学地基不牢，大厦将倾。

大家开始接受一个事实，就是在任何一组几何公理体系中，就像它必然存在某些无法证明的基本事实一样，它也必然会存在一些无法定义的概念，如点、线、面。它们无法用已知的事物定义，我们只能通过描述其性质，以描述这些基本存在。

大卫·希尔伯特(David Hilbert)

对于几何中最基本的点、线、面作为不加定义的基础概念，称之为几何的基本元素，直接用符号来表示，正如希尔伯特所说“我们必定可以用‘桌子、椅子、啤酒杯’来代替‘点、线、面’ ”，它们不再是看得见摸得着的东西来定义了，它们成了纯粹的抽象符号。同时它避开了”线是由点构成的，面是由线构成的”这一设定，将点、线、面设定成了三个独立的元素个体。
那么如何描述它们的性质，以及它们之间的联系呢？这就需要在三者之间设定一些关系和公理了。
1899年出版了《几何基础》，在这部著作中，希尔伯特创立了一个新公理系统(史称“希尔伯特公理系统”)。他从叙述20条公理开始，其中涉及六个本原概念(作为元素的点、线、面和它们之间的三种关系“属于”、“介于”、“全等于”)和五类公理，分别描述关联、顺序、全等、平行和连续性。
公理体系的标准也是希尔伯特提出来的：从不同的公理推理出来的同一个命题不能相互矛盾——一致；公理不能由其它公理推导出来，不然该公理毫无意义——独立；整个公理体系中的每个命题都能够由这些公理推理得到——完备。

希尔伯特的公理体系

The Elements：points, straight lines and planes

Let us consider three distinct systems of things. The things composing the ﬁrst system, we will call points and designate them by the letters A, B, C,…; those of the second, we will call straight lines and designate them by the letters a, b, c,…; and those of the third system, we will call planes and designate them by the Greek letters α, β, γ,…The points are called the elements of linear geometry; the points and straight lines, the elements of plane geometry; and the points, lines, and planes, the elements of the geometry of space or the elements of space.

Mutual relations

We think of these points, straight lines, and planes as having certain mutual relations, which we indicate by means of such words as “are situated(位于),” “between(介于),” “parallel(平行),” “congruent(全等),” “continuous(连续),” etc. The complete and exact description of these relations follows as a consequence of the axioms of geometry(公理描述关系). These axioms may be arranged in ﬁve groups. Each of these groups expresses, by itself, certain related fundamental facts of our intuition(每一个公理都与我们直接感受到的基本事实相关). We will name these groups as follows: I, 1–7. Axioms of connection. II, 1–5. Axioms of order. III. Axiom of parallels (Euclid’s axiom). IV, 1–6. Axioms of congruence. V. Axiom of continuity (Archimedes’s axiom).

Axioms of connection

The axioms of this group establish a connection between the concepts indicated above(这组公理建立三元素的关联); namely, points, straight lines, and planes. These axioms are as follows:
I, 1. Two distinct points A and B always completely determine a straight line a. We write AB = a or BA = a. 两个不同的点A,B总是完全确定一条直线a(点A,B在直线a上)

I, 2. Any two distinct points of a straight line completely determine that line; that is, if AB = a and AC = a, where B≠ C, then is also BC = a. 直线上的任意不同两点确定这条直线，如果点A、B在直线a上，点A、C也在直线a上，且B、C是不同的点，那么点B、C也确定这条直线(在直线a上)。
I, 3. Three points A, B, C not situated in the same straight line always completely determine a plane α. We write ABC = a.三个不在同一条直线上的点总是完全确定一个平面α(点A,B,C在平面α上)

I, 4. Any three points A, B, C of a plane α, which do not lie in the same straight line,completely determine that plane. 位于平面α的任意三点A、B、C，若不位于同一条直线上，可以完全确定该平面

I, 5. If two points A, B of a straight line a lie in a plane α, then every point of a lies in α. 如果直线a上的两点A、B位于平面α，那么直线上的所有点都位于α
In this case we say: “The straight line a lies in the plane α,” etc.
I, 6. If two planes α, β have a point A in common, then they have at least a second point B in common. 如果平面α、β都有点A，那么他们至少都有第二个点B

I, 7. Upon every straight line there exist at least two points, in every plane at least three points not lying in the same straight line, and in space there exist at least four points not lying in a plane. 每条直线上至少有2个电，每个平面内至少有3个不位于同一直线的点，每个空间内至少有4个不位于同一平面的点。

Axioms I, 1–2 contain statements concerning points and straight lines only; that is, concerning the elements of plane geometry. We will call them,therefore,the plane axioms of group I, in order to distinguish them from the axioms I, 3–7, which we will designate brieﬂy as the space axioms of this group. Of the theorems(定理) which follow from the axioms I, 3–7, we shall mention only the following:
Theorem 1. Two straight lines of a plane have either one point or no point in common; two planes have no point in common or a straight line in common; a plane and a straight line not lying in it have no point or one point in common.

Theorem 2. Through a straight line and a point not lying in it, or through two distinct straight lines having a common point, one and only one plane may be made to pass.

Axioms of order

The axioms of this group deﬁne the idea expressed by the word “between,”(这组公理定义“介于”这个词表达的含义) and make possible, upon the basis of this idea, an order of sequence of the points upon a straight line, in a plane, and in space. The points of a straight line have a certain relation to one another which the word “between” serves to describe. The axioms of this group are as follows:
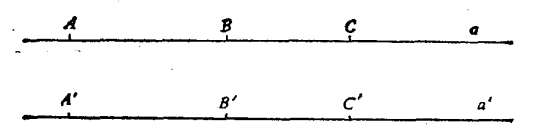
II, 1. If A, B,C are points of a straight line and B lies between A and C,then B lies also between C and A. 如果点A、B、C位于一条直线上，并且B位于A和C之间，那么B也位于C和A之间。

II, 2. If A and C are two points of a straight line, then there exists at least one point B lying between A and C and at least one point D so situated that C lies between A and D. 如果A、C是一条直线上的两点，那么存在至少一个点B位于A和C之间，并且存在至少一个点D，点D如此位于直线，使得C位于A和D之间。
Fig. 2.
II, 3. Of any three points situated on a straight line, there is always one and only one which lies between the other two. 对于位于一条直线的任意三个点，总是只有一个点位于另外两点之间。

II, 4. Any four points A, B, C, D of a straight line can always be so arranged that B shall lie between A and C and also between A and D, and, furthermore, that C shall lie between A and D and also between B and D. 任意四个位于一条直线的点A、B、C、D，总是能如此安排，B位于A和C、A和D之间，且C位于A和D、B和D之间

Definition. We will call the system of two points A and B, lying upon a straight line, a segment and denote it by AB or BA(由两点构成的，位于一条直线上的系统，称作线段). The points lying between A and B are called the points of the segment AB or the points lying within the segment AB. All other points of the straight line are referred to as the points lying outside the segment AB.(位于点A、B之间的点称作线段AB上的点，其他点称作线段AB外的点) The points A and B are called the extremities of the segment AB.(点A、B称作线段AB的边界)
II, 5. Let A, B, C be three points not lying in the same straight line and let a be a straight line lying in the plane ABC and not passing through any of the points A, B, C. Then, if the straight line a passes through a point of the segment AB, it will also pass through either a point of the segment BC or a point of the segment AC. A、B、C是不位于同一条直线上的三点，直线a是位于平面ABC但是不经过A、B、C任何一点的直线。那么，如果a经过线段AB的一点，它也经过线段BC或线段AC的一点。

Axioms II, 1–4 contain statements concerning the points of a straight line only, and, hence, we will call them the linear axioms of group II. Axiom II, 5 relates to the elements of plane geometry and, consequently, shall be called the plane axiom of group II.

Axioms of parallels (EUCLID’S AXIOM)

The introduction(使用) of this axiom simpliﬁes greatly the fundamental principles of geometry and facilitates in no small degree(不小程度的) its development. This axiom may be expressed as follows:

III. In a plane α there can be drawn through any point A, lying outside of a straight line a, one and only one straight line which does not intersect the line a. This straight line is called the parallel to a through the given point A. 在平面α中，可以经过在直线a外的一点A，画出一条且只有一条直线与直线a不相交。这个直线叫做经过给定点A的a的平行直线。

Axioms of congruence

The axioms of this group deﬁne the idea of congruence or displacement. Segments stand in a certain relation to one another which is described by the word “congruent.”
IV, I. If A, B are two points on a straight line a, and if A0 is a point upon the same or another straight line a0,then,upon a given side of A0 on the straight line a0,we can always ﬁnd one and only one point B0 so that the segment AB(or BA) is congruent to the segment A0B0. We indicate this relation by writing AB≡ A0B0. Every segment is congruent to itself; that is, we always have AB≡ AB. We can state the above axiom brieﬂy by saying that every segment can be laid off upon a given side of a given point of a given straight line in one and and only one way. 如果A、B是直线a的两点，A0是同一或另一直线a0的一点，那么，在A0给定的一侧，我们总能找到一个且仅有一个点B0，使得线段AB全等于线段B0. 我们用AB≡ A0B0表示这种关系。我们可以简介地表述上述公理：每一个线段可以布置在给定直线给定点的给定侧，以一种且仅一种方式。

IV, 2. If a segment AB is congruent to the segment A0B0 and also to the segment A00B00, then the segment A0B0 is congruent to the segment A00B00; that is, if AB ≡ A0B and AB≡ A00B00, then A0B0 ≡ A00B00. 线段AB与A0B0全等，线段AB与A00B00全等，则线段A0B0与A00B00全等。

IV,3. Let AB and BC be two segments of a straight line a which have no points in common aside from the point B, and, furthermore, let A0B0 and B0C0 be two segments of the same or of another straight line a0 having, likewise, no point other than B0 in common. Then, if AB≡ A0B0 and BC ≡ B0C0, we have AC ≡ A0C0. 线段AB和BC是直线a的两个线段，AB和BC只有公共点B，线段A0B0和B0C0是同一或另一直线a0的两个线段，同样只有公共点B0，那么，AB≡ A0B0且BC≡ B0C0，就有AC≡ A0C0

Definitions. Let α be any arbitrary plane and h, k any two distinct half-rays(射线) lying in α and emanating(产生自) from the point O so as to form a part of two different straight lines. We call the system formed by these two half-rays h, k an angle(角) and represent it by the symbol ∠(h,k) or ∠(k,h). From axioms II, 1–5, it follows readily that the half-rays h and k, taken together with the point O, divide the remaining points of the plane α into two regions having the following property: If A is a point of one region and B a point of the other, then every broken line(虚线) joining(连接) A and B either passes through O or has a point in common with one of the half-rays h, k. If, however, A, A0 both lie within the same region, then it is always possible to join these two points by a broken line which neither passes through O nor has a point in common with either of the half-rays h, k. One of these two regions is distinguished from the other in that the segment joining any two points of this region lies entirely within the region. The region so characterised is called the interior(内部) of the angle (h,k). To distinguish the other region from this, we call it the exterior(外部) of the angle (h,k). The half rays h and k are called the sides of the angle, and the point O is called the (顶点)vertex of the angle.

IV, 4. Let an angle (h,k) be given in the plane α and let a straight line a0 be given in a plane α0. Suppose also that, in the plane α0, a deﬁnite side of the straight line a0 be assigned. Denote by h0 a half-ray of the straight line a0 emanating from a point O0 of this line. Then in the plane α0 there is one and only one half-ray k0 such that the angle (h,k), or (k,h), is congruent to the angle (h0,k0) and at the same time all interior points of the angle (h0,k0) lie upon the given side of a0. We express this relation by means of the notation ∠(h,k)≡∠(h0,k0) Every angle is congruent to itself; that is, ∠(h,k)≡∠(h,k) or ∠(h,k)≡∠(k,h) We say, brieﬂy, that every angle in a given plane can be laid off upon a given side of a given half-ray in one and only one way. 角(h,k)在平面α上，直线a0在平面α0上。在平面α上，指定直线a0的一侧，由a0上一点00产生的属于a0的射线标记为h0.在平面α0上有且只有一条射线k0，使得角(h,k)与角(h0,k0)全等
IV, 5. If the angle (h,k) is congruent to the angle (h0,k0) and to the angle (h00,k00), then the angle (h0,k0) is congruent to the angle (h00,k00); that is to say, if ∠(h,k) ≡∠(h0,k0) and ∠(h,k)≡∠(h00,k00), then∠(h0,k0)≡∠(h00,k00). 此时所有角(h0,k0)内部的点都位于直线a0指定的一侧。我们用标记 ∠(h,k)≡∠(h0,k0)表达这种关系，每个角都全等它自己, 即∠(h,k)≡∠(h,k) 或 ∠(h,k)≡∠(k,h)。我们简单的说，在给定平面上的每个角可以被转移到指定射线的指定一侧，有且仅有一种方式。

Suppose we have given a triangle ABC. Denote by h, k the two half-rays emanating from A and passing respectively through B and C. The angle (h,k) is then said to be the angle included by the sides AB and AC, or the one opposite to the side BC in the triangle ABC. It contains all of the interior points of the triangle ABC and is represented by the symbol ∠BAC, or by ∠A.

IV, 6. If, in the two triangles ABC and A0B0C0 the congruences AB≡ A0B0, AC ≡ A0C0, ∠BAC ≡∠B0A0C0 hold, then the congruences ∠ABC ≡∠A0B0C0and∠ACB≡∠A0C0B0 also hold. 如果再两个三角形中，两边全等，其夹角也全等，那么另外两个角也全等

Axioms IV, 1–3 contain statements concerning the congruence of segments of a straight line only. They may, therefore, be called the linear axioms of group IV. Axioms IV, 4, 5 contain statements relating to the congruence of angles. Axiom IV, 6 gives the connection between the congruence of segments and the congruence of angles. Axioms IV, 4–6 contain statements regarding the elements of plane geometry and may be called the plane axioms of group IV.

Axioms of continuity To Do

姑且不谈，先看实数的连续型，即可比数和不可比数在数轴上的分布情况。

希尔伯特怎么证明其几何公理体系的一致性，独立性，完备性 To Do

坑待填

哥德尔不完备性定理 To Do

那一年是1931年，希尔伯特的几何公理体系面世三十年之际，奥地利数学家、逻辑学家、哲学家库尔特∙哥德尔（Kurt Gödel，1906—1978）发表了一篇论文，这一篇论文中的定理就是数学和逻辑学中具有划时代意义的定理——哥德尔不完备性定理.

在这个定理中，哥德尔证明了任何一个形式系统(希尔伯特的几何公理体系正是一个几何的形式化系统)，只要包括了简单的初等数论描述，而且是自洽的，它必定包含某些系统内所允许的方法既不能证明真也不能证伪的命题.

呃，有点绕，我们说得再直白点，前面我们说到，希尔伯特所建立的几何公理体系有三大基本标准：相容性，独立性，完备性. 而哥德尔不完备定理则证明了这三个标准无法同时具备，即如果公理体系满足相容性，那么它就不可能是完备的. 换句话说，在一个不存在矛盾的公理体系中，必然存在某些命题没办法证明其是真的还是假的.(当然这些命题只是在这个公理体系中无法证明，并不代表它们在其它公理体系中也不能证明.)

至于哥德尔怎么证的，尚且不知，坑待填

非欧几何-球面几何，双曲几何

再说回到欧几里得几何，在欧几里得的几何公理体系中，那个更致命的问题是什么？

答案是：平行公设.

我们来看欧几里得的公理体系中的五条公设：

★ 1.过两点能作且只能作一直线； 2.线段(有限直线)可以无限地延长； 3.以任一点为圆心,任意长为半径,可作一圆； 4.凡是直角都相等； 5.同平面内一条直线和另外两条直线相交，若在直线同侧的两个内角之和小于180°，则这两条直线经无限延长后在这一侧一定相交.
”

仔细观察会发现，前面四条讲的都是在有限范围内的图形，我们是可以直观上观测并验证的基本事实，然而第五条就不一样了，“经过无限延长后在这一侧相交”，无限延长？你能看见尽头？你怎么验证其是否真的相交了？

这条公设引起了无数数学家们的注意，既然无法验证，那么，是否可以由其它几条推出这条呢？如果可以的话，就说明这条公设并不具备独立性，我们就可以把它拿下来，不再作为公理了. 于是数学家们前赴后继，想要证明这一条，却屡屡失败. 终于，数学家们开始意识到，这个公设确实是独立的.

那么，既然它是独立的，我们就可以尝试建立一个相似的公理体系，其它公设都依然成立，唯独不满足平行公设，1830年Lobachevsky和Bolyai给出了两个不同的几何模型。

非欧几何诞生了.

至此，几何学开始分裂了，也开始蓬勃发展了.

非欧几何我们陌生吗？并不陌生，它和我们生活息息相关. 举个简单例子，拿个地球仪观察一下，南北极之间有几条平行线？

答：无数条. 每一条经度线都平行. 这就是不满足平行公设的球面几何，也是非欧几何的一种