微积分
参考台湾大学的微积分课程-陈金次教授
Youtube-Stepp学院
Youtube-冉哥 参考书《Principles of Mathematical Analysis》Third EDITION by Walter Rudin
Youtube-李永乐
知乎,百度
一、《Principles of Mathematical Analysis》Chapter1 结合冉哥视频
公理化数集,繁琐,严谨,但不直观,建议跳过。
集合
从习惯上的自然数、可比数及其加减乘除次方运算,发展到用集合定义数集,定义运算
集合,元素,常见数集
把你感兴趣的东西放在一起,被放到一起的东西叫element(元素),整体称为Set(集合)。
元素符合的条件:不重复,无顺序。
元素和集合的关系:元素∈(属于)或∉(不属于)一个集合。
集合和集合的关系:如果一个集合的元素,总是属于另一个集合,称该集合包含于另一个集合,若两集合不相同,则成该集合真包含于另一个集合。
常见的数集:
- N 自然数集:0, 1, 2, 3, …
- Z 整数集:…, -3, -2, -1, 0, 1, 2, 3, …,在N的基础上增加负数
- Q 可比数集:1, 1.1, 1.11, 1/2, 1.232323…, …
- R 实数集:根号2,π,e,… 在Q的基础上增加不可比数
超越实际世界之处:集合的元素,可以是无穷多个的(没有确定的上界,总能找到更大的元素)
无尽:没有尽头,假设一个尽头,总能找到尽头之外的东西。
稠密:指定一个点,无法指定邻点,如果指定邻点,总能找到更近的邻点。
集合的运算
集合与另一个集合做运算,产生新的集合
Union(联合) AUB={a|a∈A or a∈B}
Intersection(相交) A∩B={a|a∈A and a∈B}
Complement(补) A-B={a|a∈A and a∉B}
集合的运算性质
集合的运算性质建立在逻辑运算(and or not)的运算性质上,逻辑运算的运算性质是观察真实世界后,规定出来的,是不可证的公理。
- commutative law 交换律:
AUB=BUC,A∩B=B∩A
- associative law 结合律:
AU(BUC) = (AUB)UC
A∩(B∩C) = (A∩B)∩C
- distributive law 分配率:
AU(B∩C) = (AUB)∩(AUC)
A∩(BUC) = (A∩B)U(A∩C)
有序集
Ordered Set 集合中的元素可以比大小
Order:(i)x∈S,y∈S,要么x<y,要么x=y,要么x>y。
(ii) if x<y and y<z,then x<z
上界和最小上界
S是一个有序集,E包含于S,如果β∈S,使得对E集合中的任意元素x都有,x≤β,称β为E的上界
α是E的一个上界,如果r<α,则r不是E的上界,则α是E的最小上界。


类似的,S是一个有序集,E包含于S,如果β∈S,使得对E集合中的任意元素x都有,x≥β,称β为E的下界
α是E的一个下界,如果r>α,则r不是E的下界,则α是E的最大下界。
平方平均 算术平均 几何平均 调和平均(勾股定理,相似,切线)
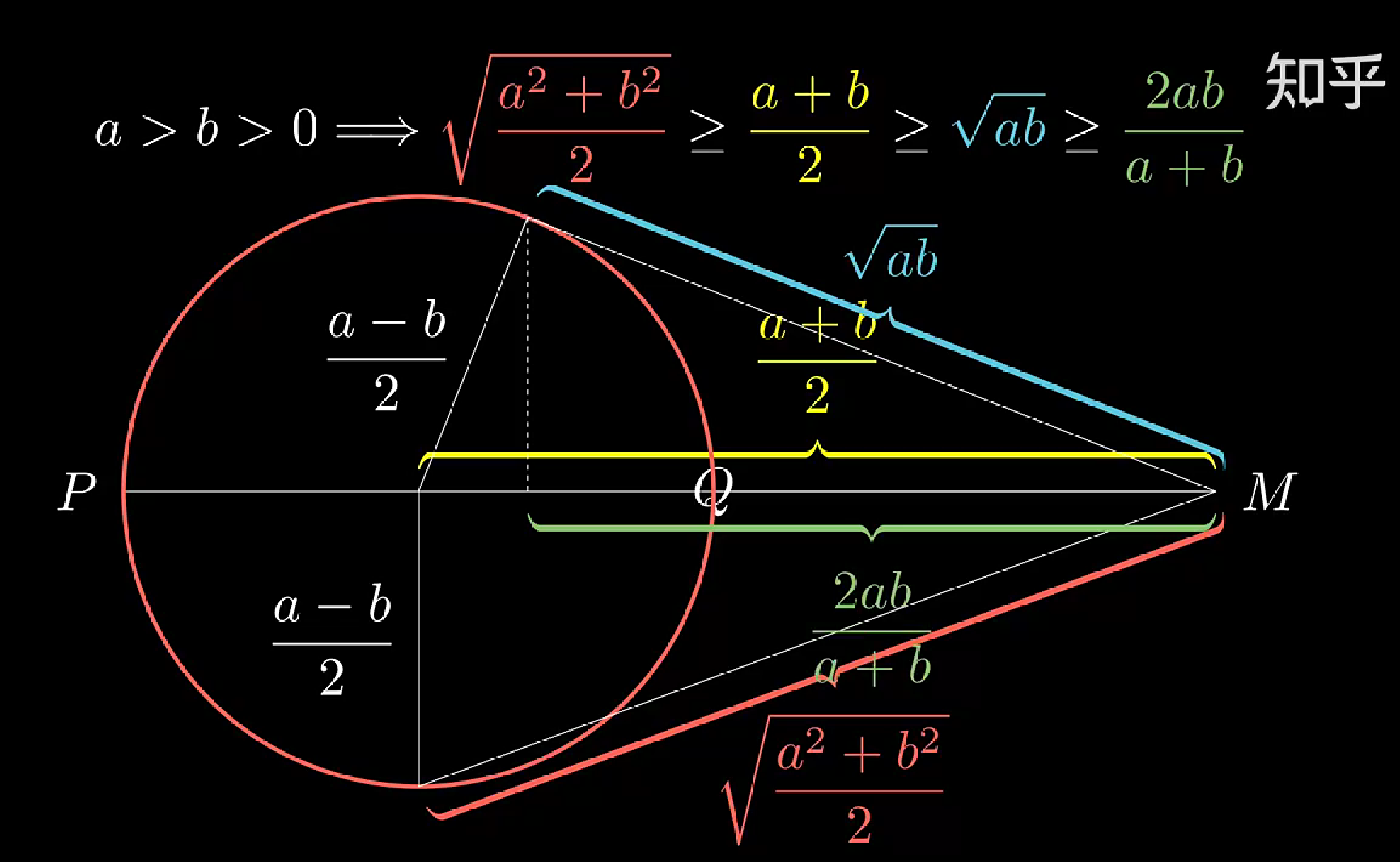
圆的切线垂直于过切点的半径

最小上界性质
如果对于有序集S(元素可比较大小),S的任意子集E非空,E有上界,则E有最小上界,称有序集S具有最小上界性质
Q没有最小上界性质,因为其子集{x|x∈Q and x^2<2}没有最小上界。
定理:确界性定理
如果一个集合具有最小上界性质,那么它也具有最大下界性质
自己的思考
将所有感兴趣的数组成一个集合,这个数集中的所有点挤在一起形成了数轴,数轴的左右或许有或许没有尽头,截取数轴的一小段或许有或许没有尽头。
无尽:没有尽头,假设一个尽头,总能找到尽头之外的东西。
稠密:指定一个点,无法指定邻点,如果指定邻点,总能找到更近的邻点。
自然数是无尽的,但不稠密的;可比数是无尽的,稠密的。
可以分情况讨论:
- S集合是不稠密的
- S集合是稠密的,B有最小元素

- S集合是稠密的,B没有最小元素
域Field
域是一个集合,有两个操作 + ·,并且符合域公理(field axioms)
如果元素都是数,这个域称为数域
证明 2x2=4
证明 x+y=x+z=>y=z
有序域
有序集是元素可比较大小的集合,域是元素符合域公理的集合,如果一个集合有序,且符合域公理,且符合
(i)y<z => x+y<x+z
(ii) x>0 and y>0 => xy>0
称该集合为有序域
证明 1>0
实数的构建 Dedekind Cuts
100多年前,实数的存在问题才被戴德金,柯西,康托等人解决。
戴德金分割,构建实数集
Theorem 1.19:There exists an ordered field R which has the least-upper-bound property. Moreover,R contains Q as a subfield. 存在一个有序域R,有最小上界性质,且可比数集是它的子集。
证明共9步,没写完。
证明:第一步,定义实数集合的元素为分割
第二步:定义分割的真包含关系为实数的小于关系,则实数集满足有序集的条件,实数集是一个有序集
第三步,证明实数集有最小上界性质
第四步,证明实数集符合域的加法公理
第五步,证明R符合有序域的性质1
第六步,证明R+满足域的乘法公理,分配律和有序域的性质2
第七步,拓展R满足域的乘法公理和分配律
第八步,定义可比分割与可比数一一对应
第九步,Q是R的真子集
注:完整过程就先不写了,太多了。
自己的思考-数的发展
从朴素的公认的自然数,加减乘除运算;
到古希腊人的尺规作图产生可比数(通过相似);
再到尺规作图产生不可比数(勾股定理或相似);
再到使用集合,有序集合,域,有序域及其公理的定义,构建了数集的公理化体系,使实数集在可比数集之上产生。
实数的阿基米德性质
可比数在实数集合中是稠密的
二、李永乐讲戴德金分割
自然,直观,美!
人们发现可比数之间有空隙,戴德金分割是对可比数集的分割,通过这种分割,找到了所有可比数的空隙——不可比数。定义实数集由所有的可比数及不可比数构成。此时,进行同样的分割,可比数集的空隙(不可比数)已经在实数集中,不会切出不在实数中的数,所以说实数是完备的(连续的)。
可比数
1.什么是可比数?p=m/n,m和n都是整数且n≠0,称p是可比数。
2.可比数的稠密性:任意两个可比数之间有无穷多个可比数。
从数轴的角度看,毕达哥拉斯认为,数轴上的所有点都是可比数,可比数是稠密的,也是连续的 。
3.有理数是不完备的(不连续的)
如何定义不可比数是一个困难的问题,以至于很多年来有很多数学家拒绝承认不可比数是数。
19世纪末20世纪初的时候,轰轰烈烈的数学公理化运动开展之后,它才真正解决了。从第一次发现不可比数,造成第一次数学危机,到不可比数如何定义的问题被解决掉,一共花了两千多年。
数学公理化
从第一次数学危机,人们讨论什么是根号2,第二次数学危机,人们讨论什么是无穷小。人们就觉得数要有基础,你必须告诉我数到底是什么。
通过戴德金的方法——戴德金分割,来思考一下数学的公理化。
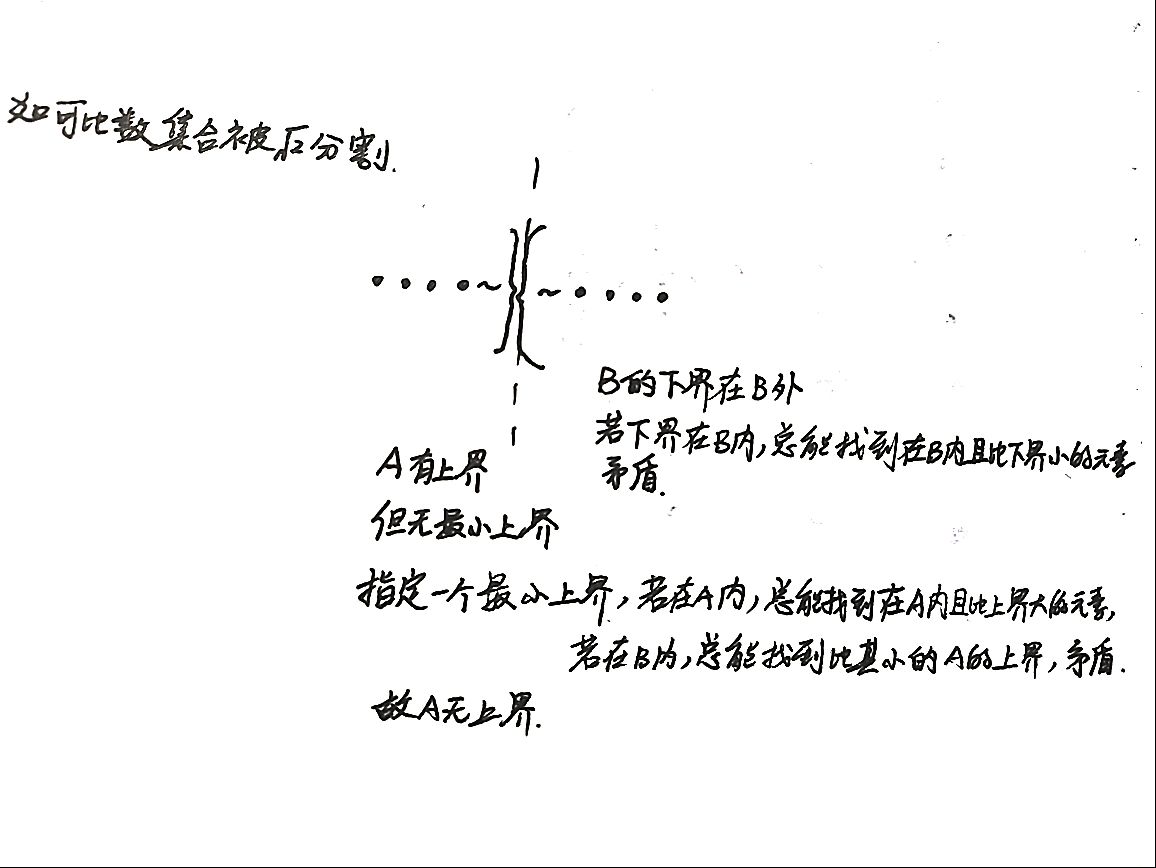
1.戴德金分割:
我们认为,数轴上有无穷多个可比数,我们称所有可比数的集合为Q,我们在数轴上切一刀,将可比数集合分成两段,一个是集合A,一个是集合B。
①分割的A与B,A∩B=∅,AUB=Q,即A和B没有重复元素,A和B包含所有的可比数。
②a∈A,b∈B,则a<b,即集合A在集合B的左侧
2.分割结果:
①A中有最大,B中无最小
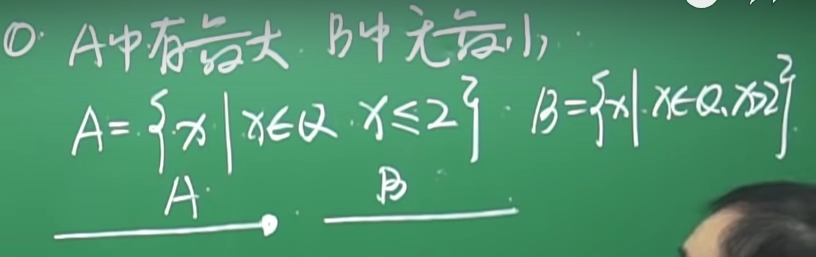
②A中无最大,B中有最小

③A中无最大,B中无最小
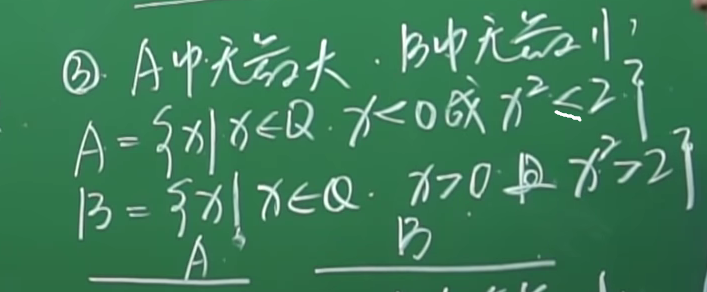
④A中有最大,B中有最小(不存在)
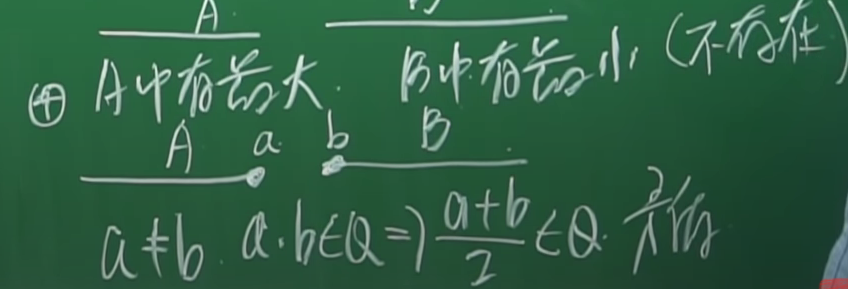
共有三种情况,在①和②中,切一刀,分割点是可比数,A和B有一个端点是可比数。在③中,切一刀,分割点不是可比数,A和B都无端点,说明这一刀从可比数的空隙钻过去了。怎么填补这个空隙,戴德金说我们定义一种数叫不可比数,不可比数就是可比数的空隙。
3.可比数的全体分割构成实数
4.戴德金推出这样一个定理:对实数进行分割,分割点只有①②两种情况,即A和B有一个端点是实数。切一刀,不可能切出一个其它的数出来,因此实数是完备的(连续的)。
证明0.999…=1
1.分割Q为A和B,定义0.999…(即割点为0.999…),分割Q为C和D,定义1
A={x|x∈Q,x<0.999…},C={x|x∈Q,x<1}
要证明0.999…=1,即证明这两种分割是一样的,即证这两个集合是一样的
2.证明A=C
①设t∈A,则t<0.999…,根据十进制数定义,0.999…不可能比1大,故0.999…≤1,t<0.999…则t<1,即t∈C。故A包含于C。
②设t∈C,t<1,t=q\p<1=>p<q ,p和q∈正整数集
1-t=1-(p/q)=(q-p)/q≥1/q
存在n,使得10^n>q=>1/10^n<1/q
1-t≥1/q>1/10^n => t<1-1/10^n=0.999…9(小数点后n位9)<0.999…,故 t∈A,C包含于A
综上所述,A=C,0.999…=1
三、微积分的基石是什么?陈金次 太长了,东西太多了,而且是倒序讲,为什么不顺序讲呢?虽然很系统,但超出了我能接受的范围,不符合我的口味。
由微积分基本定理来溯源看看
微积分第一基本定理
微积分第二基本定理
问题:
Mean Value Theorem
均值定理(微分)
均值定理(积分)
问题3的回答
连续函数中间值定理,最大最小值定理
连续函数
实数集的上界和最小上界
实数的完备性(completeness of real numbers)(实数无坑无洞)
有理数不具备完备性(有理数坑坑洞洞)
实数完备性的另一陈述
实数的构建 陈金次
什么是实数?
实数为什么有完备性?
1860年 德国数学家 R Dedekin
实数完备性与极限
数学上严格的陈述如下
最大正整数不存在
实数到底是什么?
Dedekind cut 戴德金分割
Dedekind(1831-1916)
1860年 实数的建构
他把可比数分成两个集合,所有的分割产生实数
可比数集合A无最大元素,可比数集合B若有最小元素,则该Cut决定一个可比数,可比数集合若无最小元素,则该Cut决定一个不可比数
Cut处理四则运算稍繁,故后人修改,以有上界的可比增数列来定义实数
加法
well-defined问题
区间套定理
B-W定理
连续函数中间值,最大最小值
均值定理
微积分第一第二定理
四、Stepp学院谈不可比数和极限
不可比数
无理数的发现
毕达哥拉斯:All is number 万物皆数(可比数),认为数轴由无数个可比数构成,没有空隙。
Hippasus:数轴似乎不是只由可比数构成的。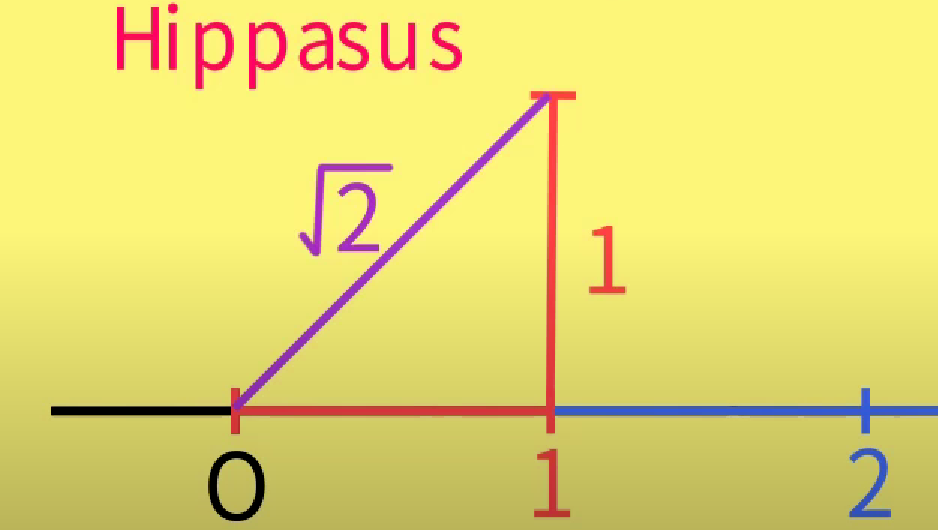
如果数轴是只有可比数构成的数轴,那么f(x)=x^2-2与数轴就无交点
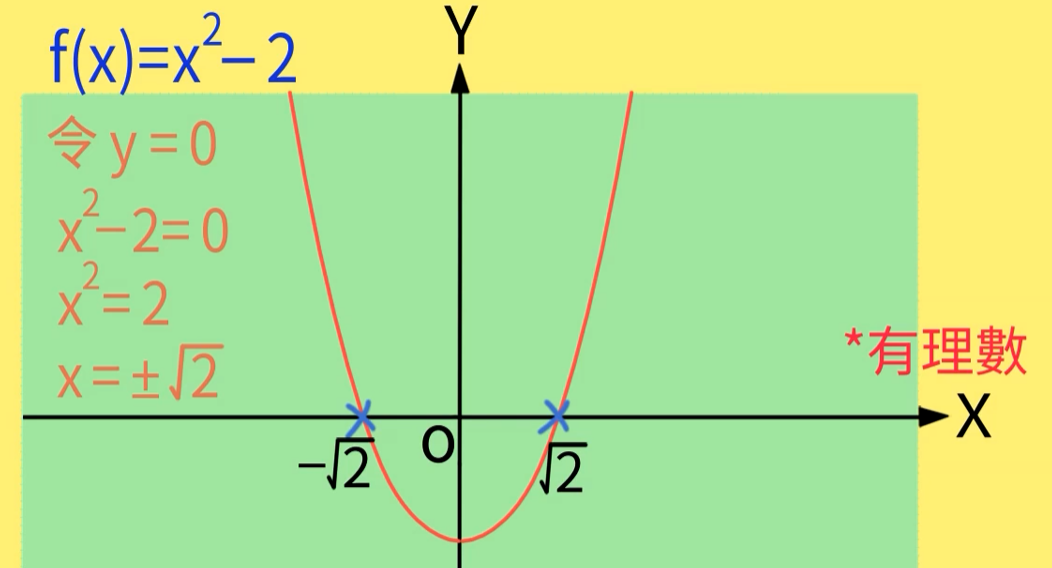
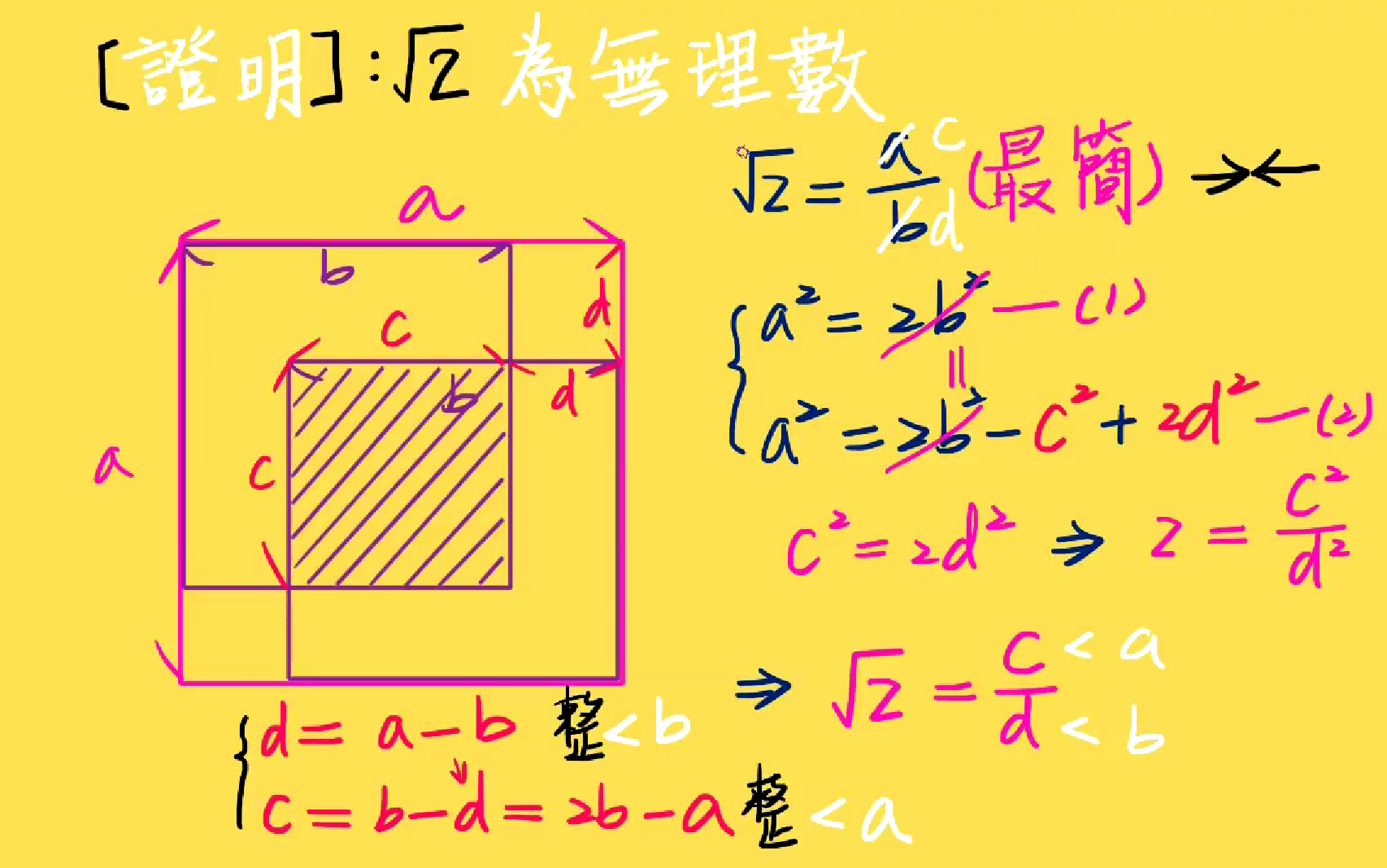
证明根号2是不可比数
代数方法:
几何方法
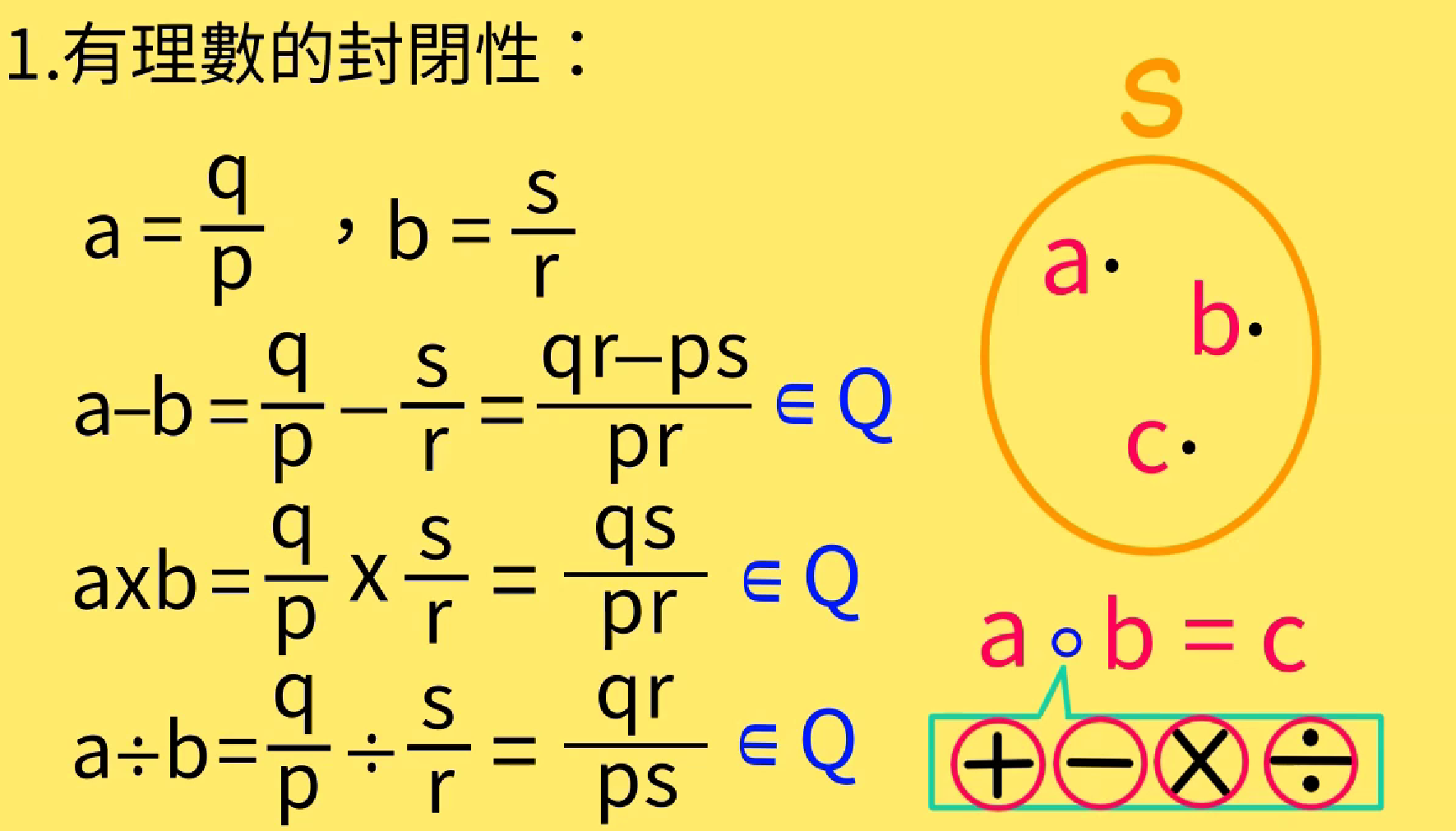
可比数不可比数的封闭性和稠密性
可比数的封闭性
可比数加减乘除运算之后还是可比数
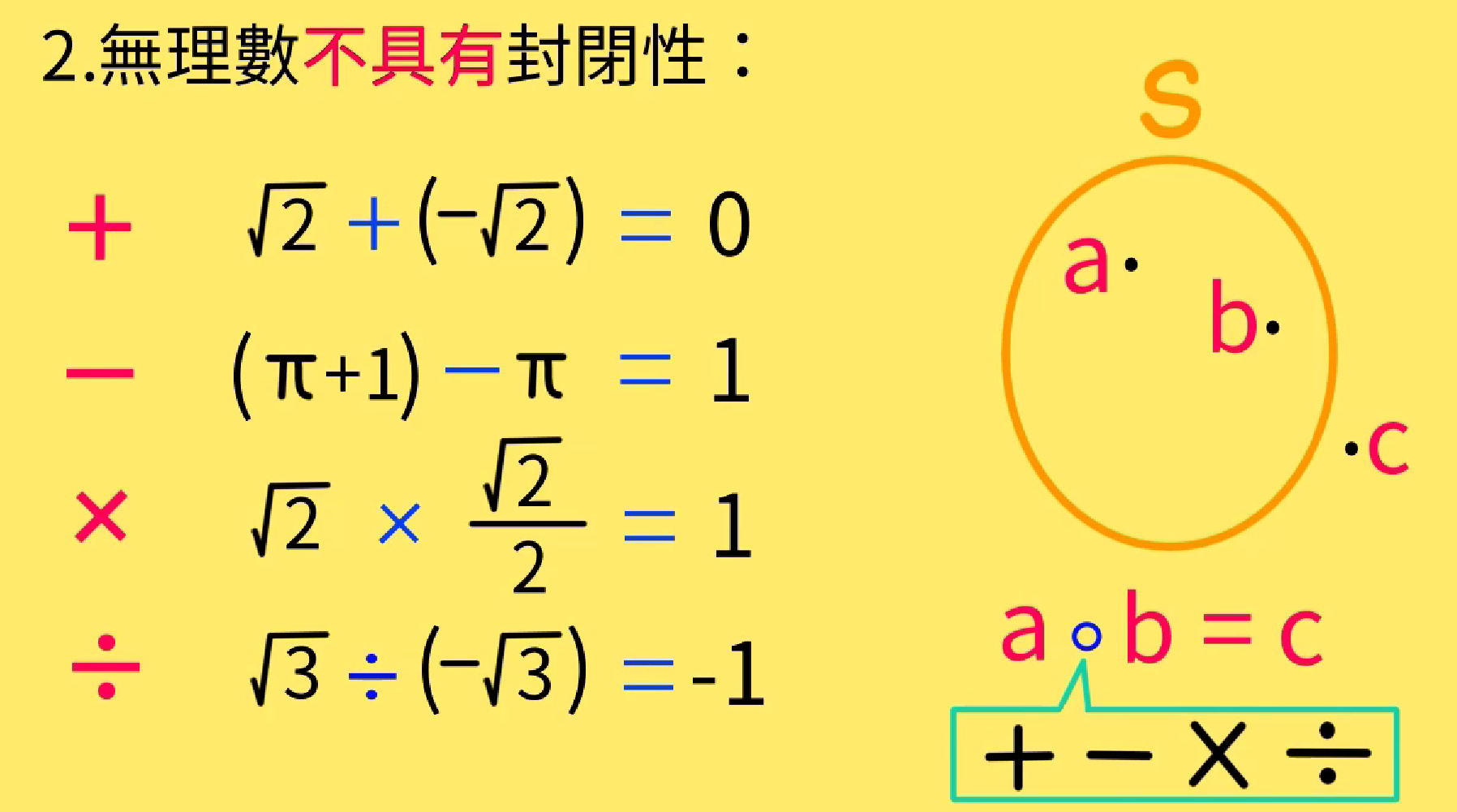
不可比数不具有封闭性
不可比数加减乘除运算之后不一定是不可比数
可比数的稠密性
两可比数之间总能找到新的可比数
整数就不具有稠密性,因为两个整数之间不总能找到新的整数

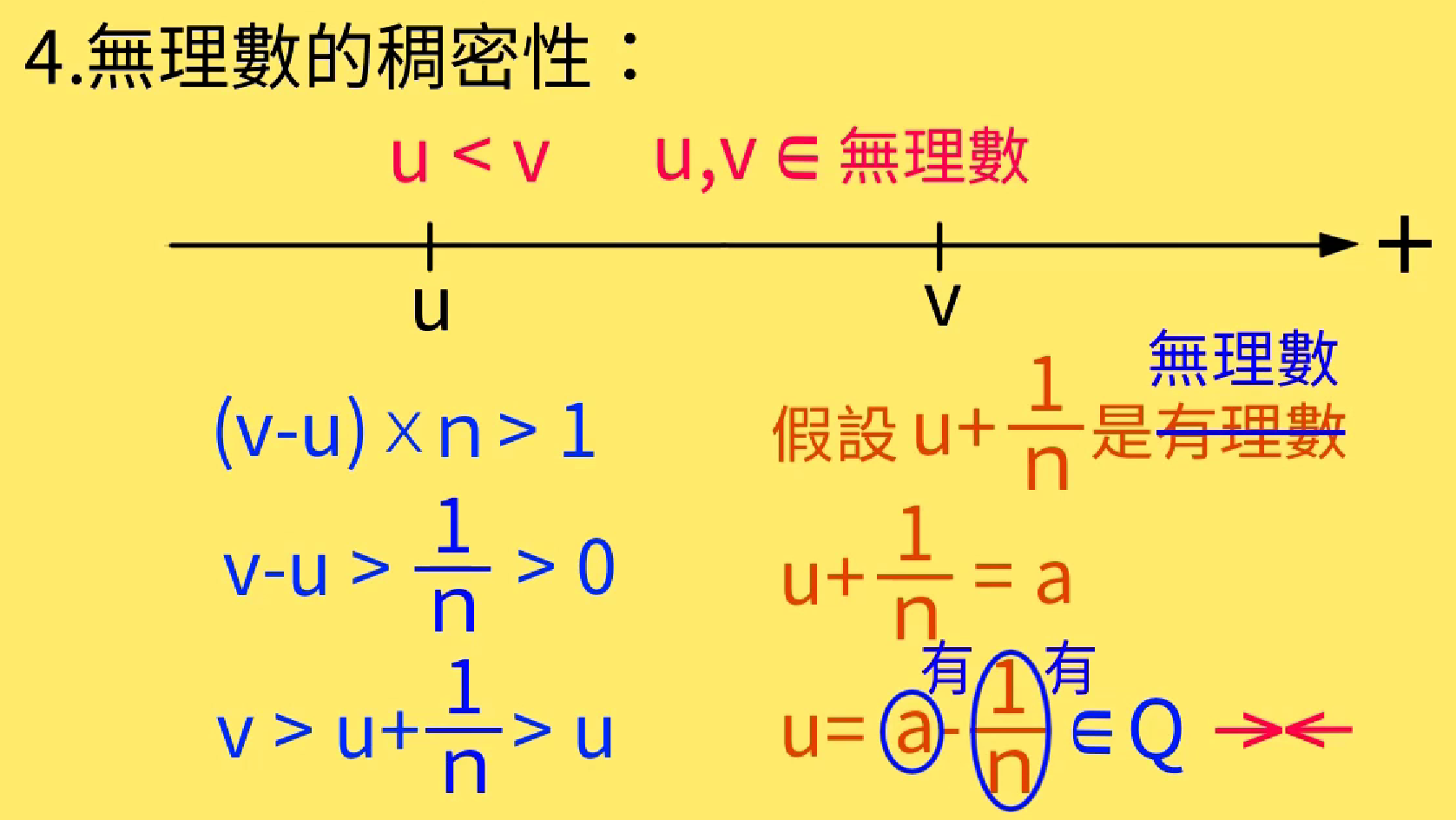
不可比数的稠密性
两不可比数之间总能找到新的不可比数
极限,x趋于某点时,函数的界限。 左极限,x从左侧趋于某点时,函数的界限。右极限,x从右侧趋于某点时,函数的界限。
切线斜率问题
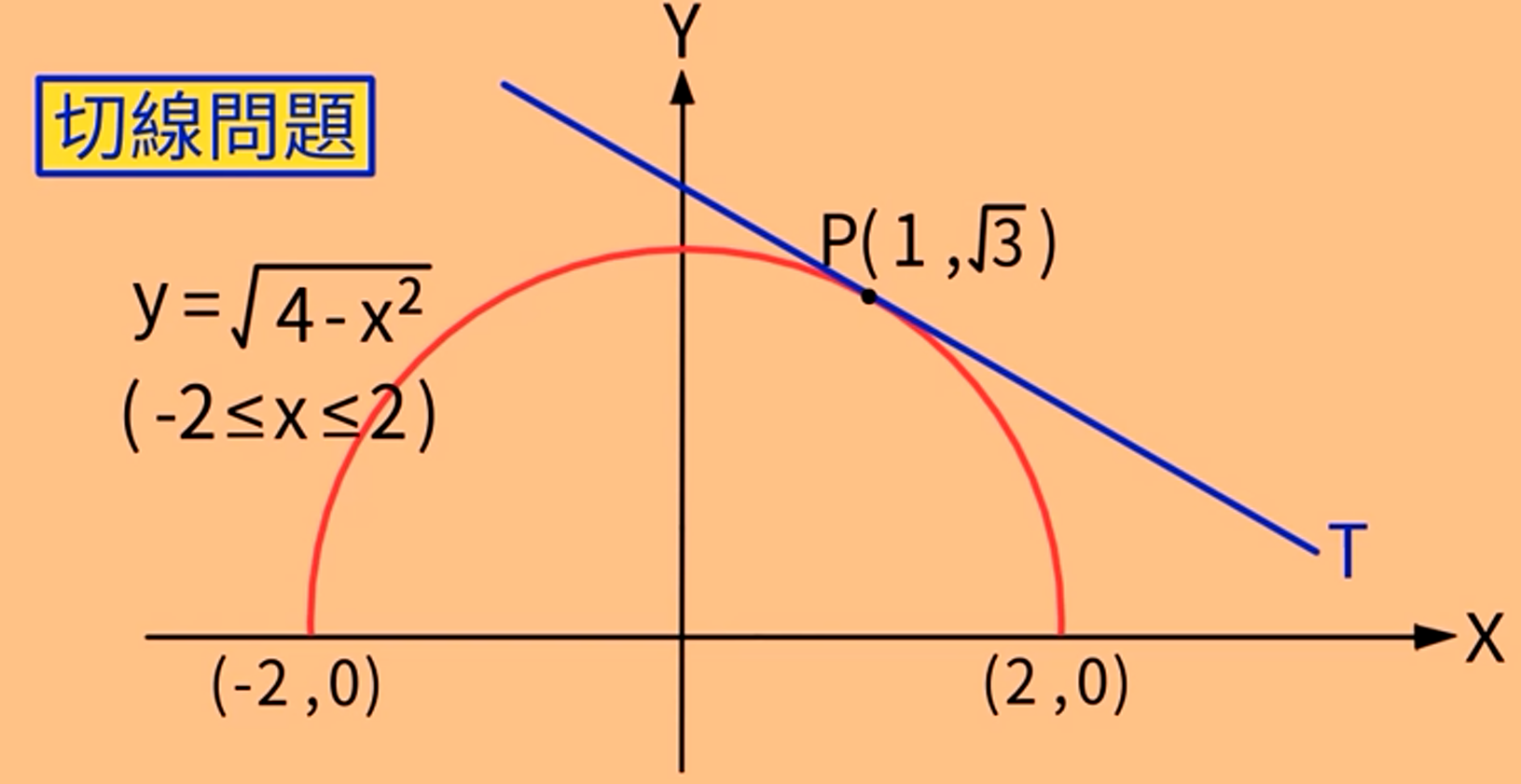
求过曲线上一点的切线P的斜率。
使用三角函数可以证明:互相垂直的直线,且直线不在坐标轴上,斜率乘积为-1。
但你不一定知道垂直于切线的直线的斜率。
我们知道,两点确定一条直线,知道两个点的坐标,才能知道直线的斜率,可切线只知道一个点,让人不知道怎么处理才好。
极限的概念就是为了解决这种切线问题所产生的。
退一步,从割线开始思考
假设曲线上有不同于P点的一点Q,则过PQ两点的S为曲线的割线,Q越接近P,割线S就越接近切线T。
当Q点非常非常接近P点的时候,割线S几乎和切线T重叠。也就是说切线T是割线S往切线T逼近的极限,或者说界限(bound)。
我们设法求出割线S的界限,也就找到了切线T。这个求界限的方法,也就是极限概念想要深入探讨的主题。
看5个函数,来认识极限的定义
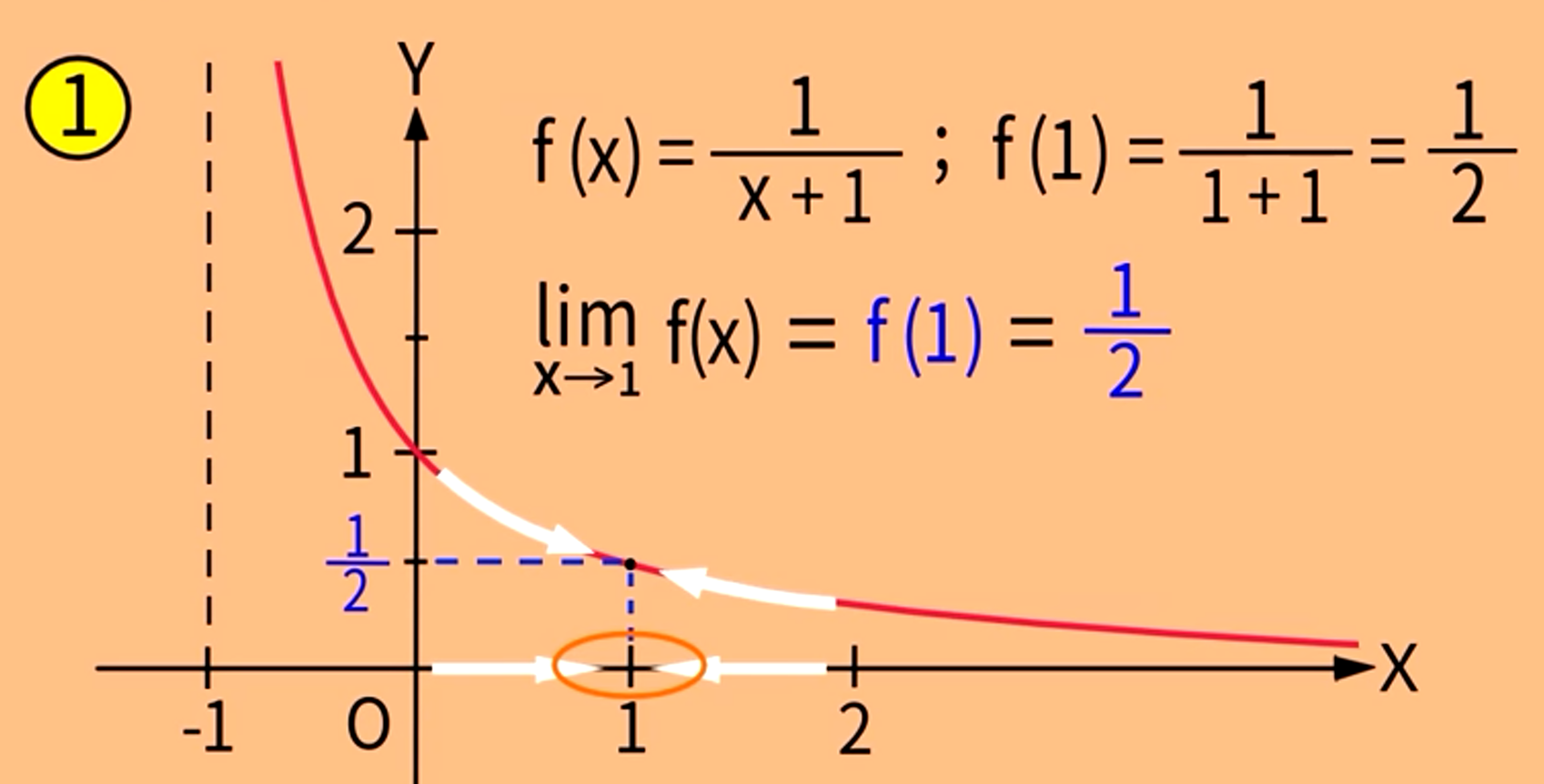
x从左趋近1,从右趋近1,看曲线f(x)的行为,也从左从右趋近1/2
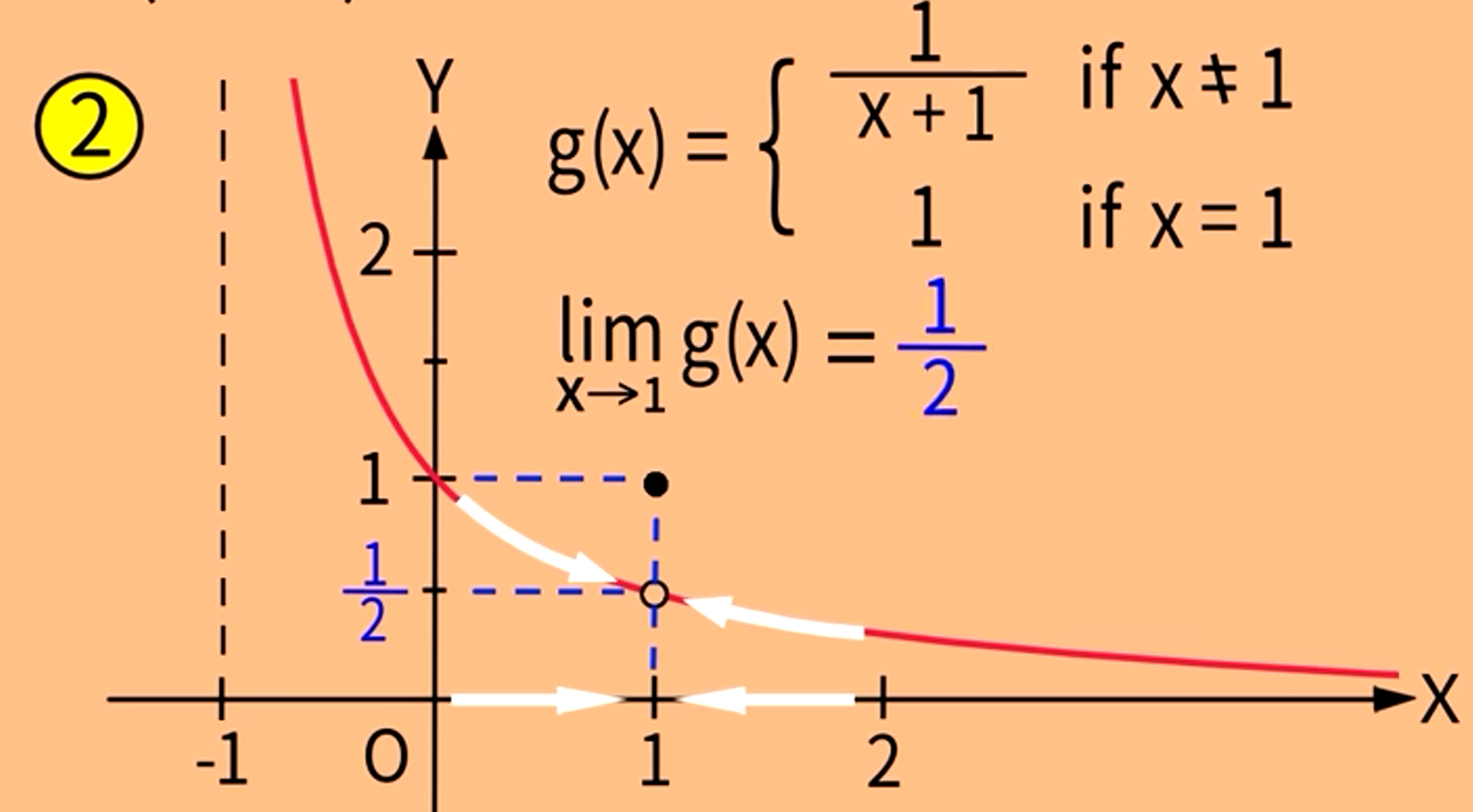
x从左从右趋于1时f(x)的值,无关f(1)的值,f(x)也从左从右趋进1/2
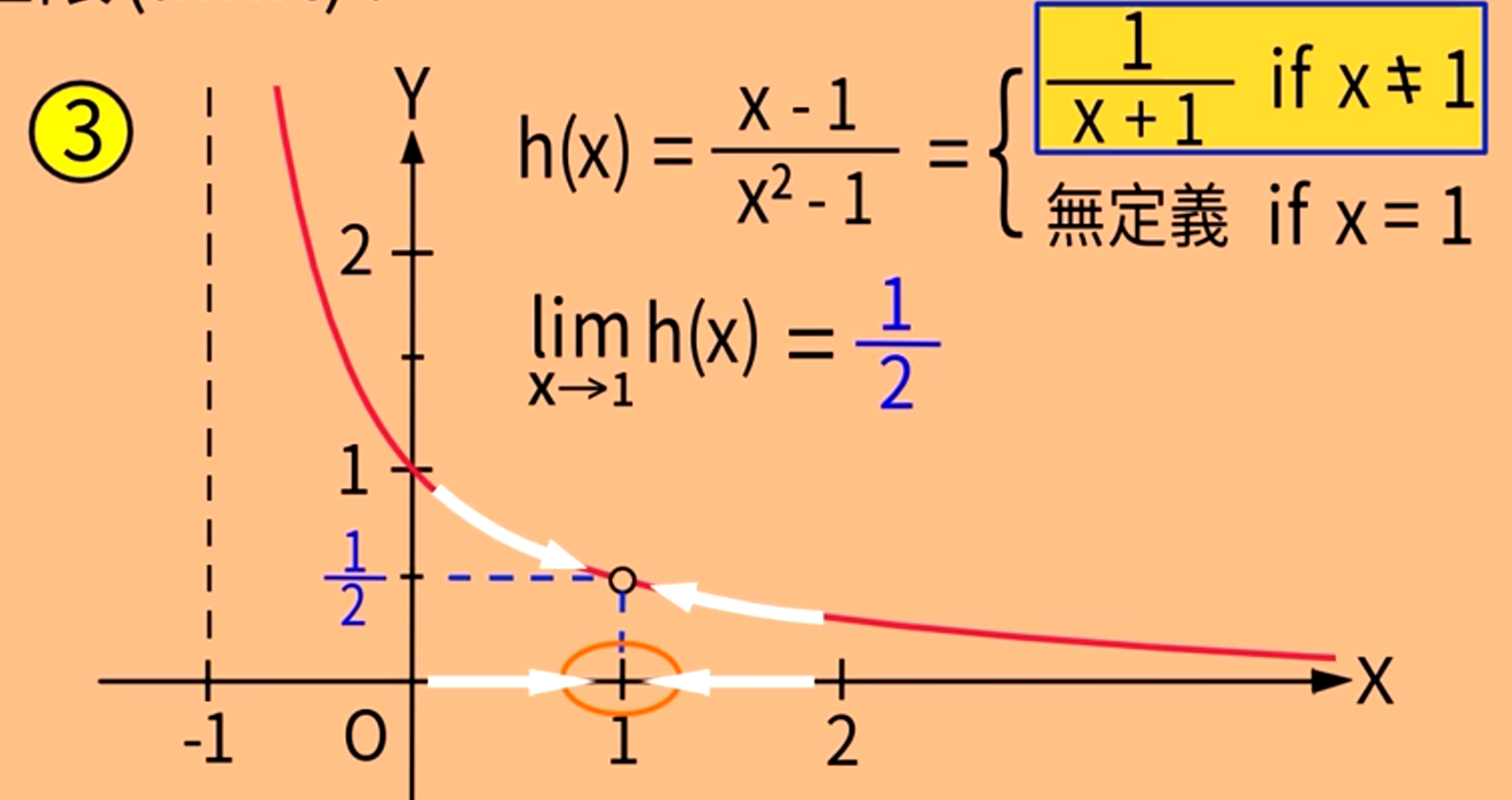
小结:

1.x趋于一点时,f(x)趋于的极限值与该点处的值无关。
2.若h(x)和f(x)仅在点a处的值不同,x趋于点a,h(x)和f(x)趋于的极限值相同
3.x趋于点a,f(x)趋于L,等同于,x从左趋点a,f(x)趋于L 且 x从右趋近点a,f(x)趋于L。
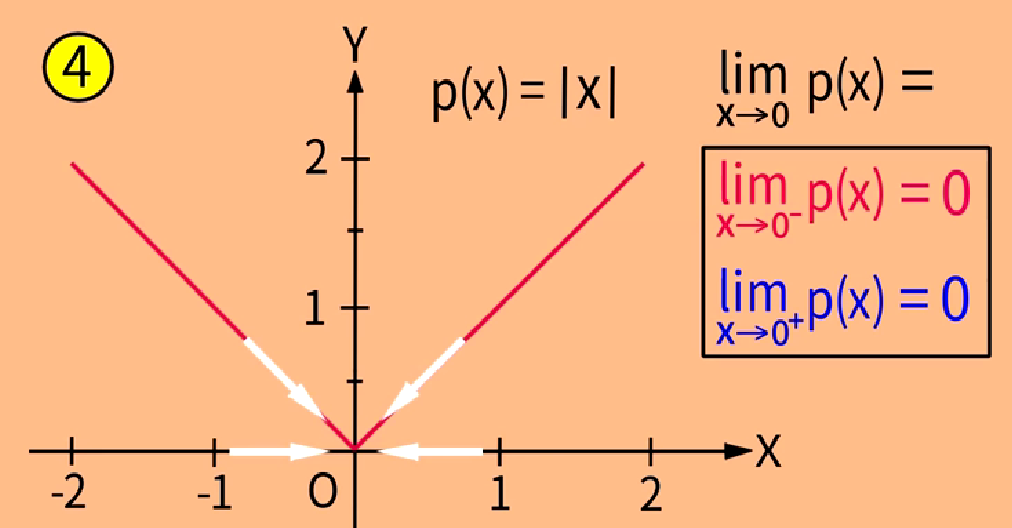
x从左从右趋于0,f(x)从左从右趋于0。
f(x)值域是和定义域中的x一一对应的集合,的左上界和右下界极限为0,定义域从0处分为左右,f(x)也从f(0)=0处分为左右,f(x)左边的最小上界为0,f(x)右边的最小下界为0(实数有最小上界和最小下界)
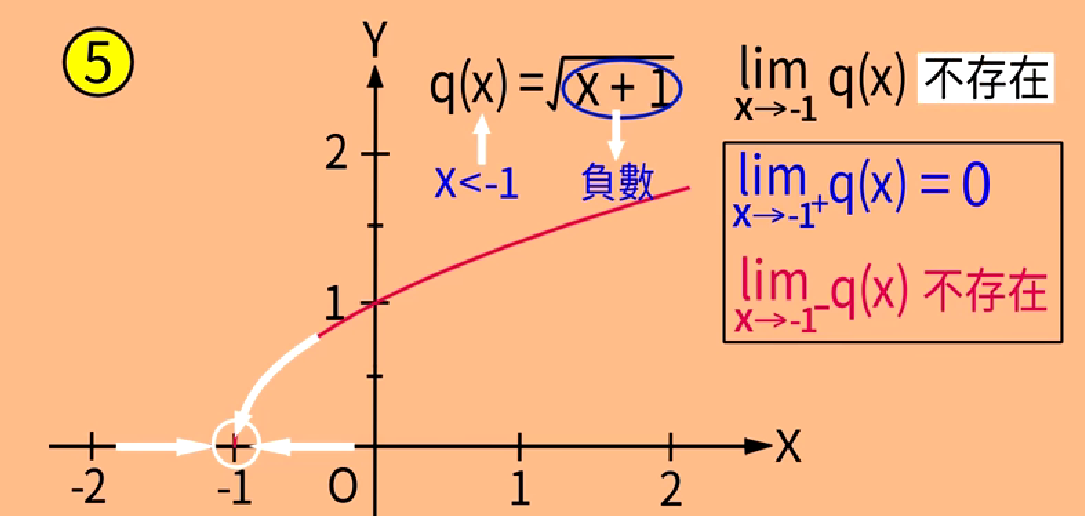
x从左侧趋于-1,f(x)在-1左侧无定义,f(x)的值在-1左侧没有行为,故x从左侧趋于-1时,f(x)没有bound(极限),称f(x)没有左极限。
x从右侧趋于-1,f(x)的值趋于0,称x趋于-1,f(x)右极限为0
回到求切线斜率问题
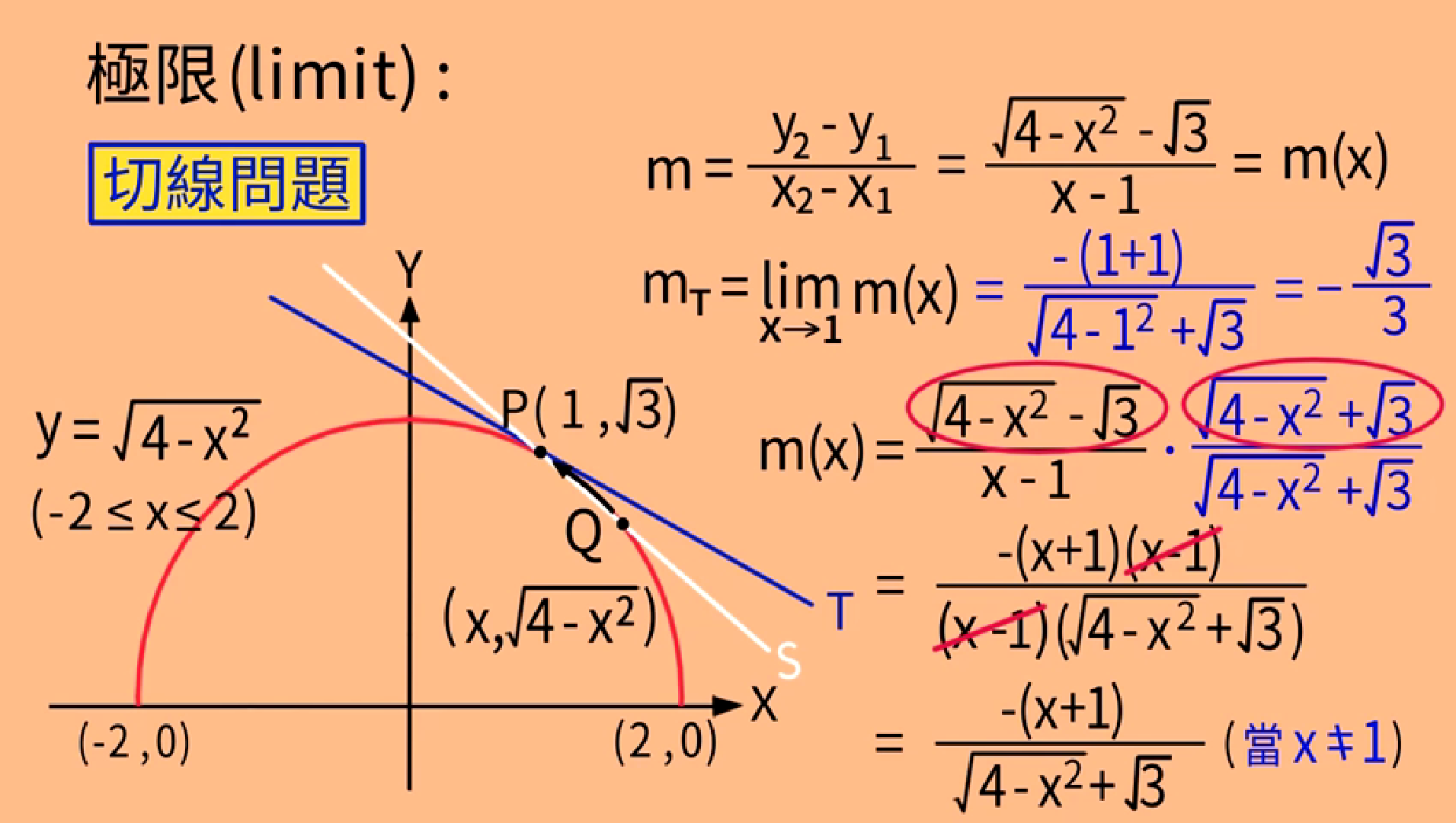
分子和分母约去x-1后的函数,与m(x)不是同一个函数,但是x趋于1时两函数的界限相同(替代定理)
极限的ε-δ定义
Fermat和Newton使用无穷小量o求切线斜率
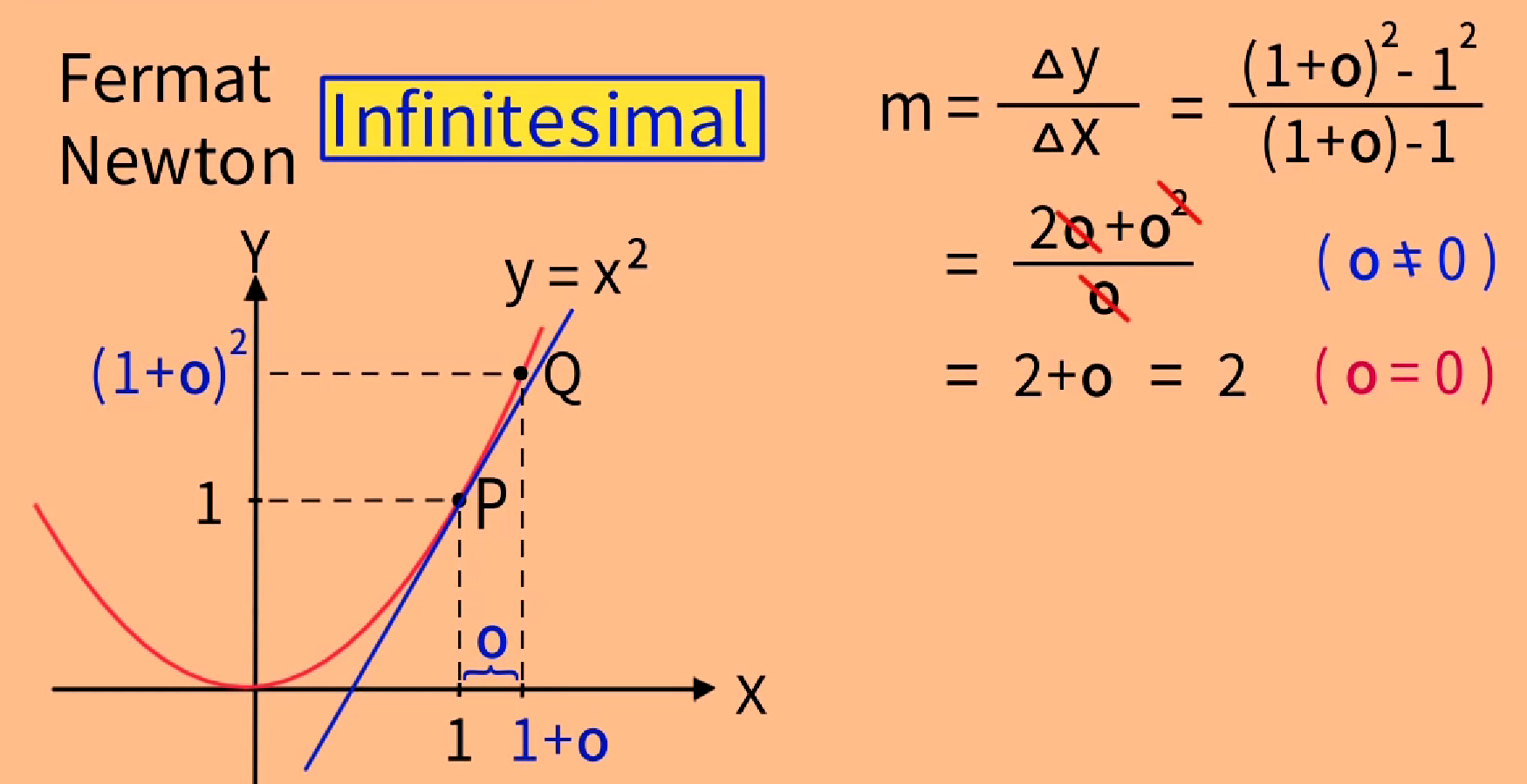
Stepp学院的直观求法
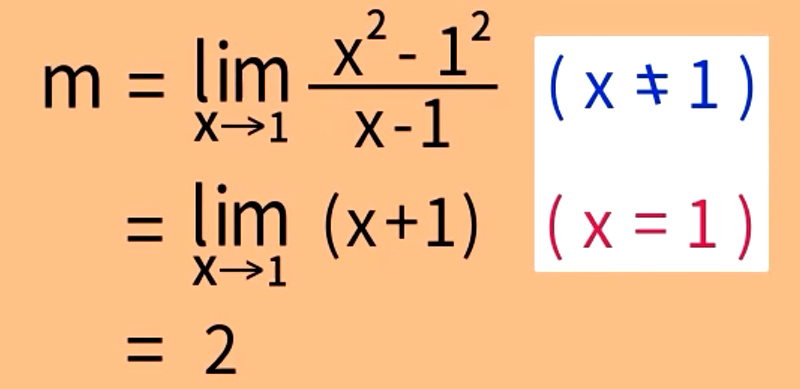
缺陷
无穷小量o,先是o≠0约分,约分后又说o=0。
定义域中的x,先是x≠1约分,约分后又说x=1。
虽然这样做,最后的结果是对的,应用上也取得成功,但这个做法是有矛盾的。
极限的严谨的定义
Cauchy,Bolzano,weierstrass,Cantor等人给出了极限的严格定义,无穷小量的争议和矛盾才解决了,微积分才可以在一个稳固的基础上做发展。
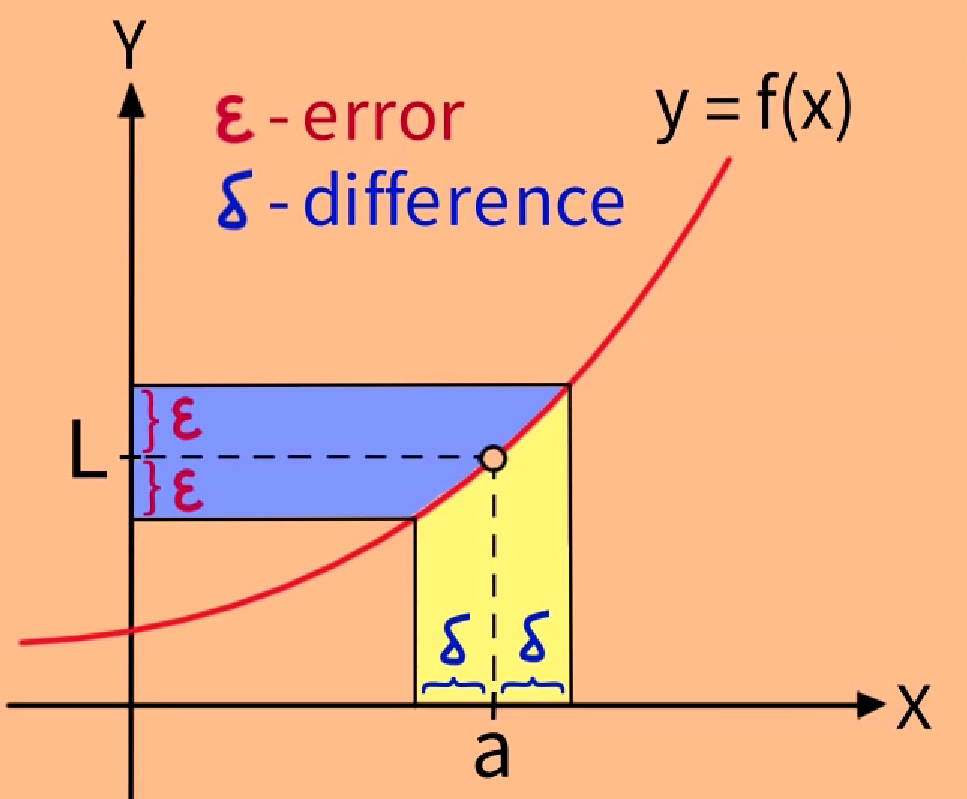
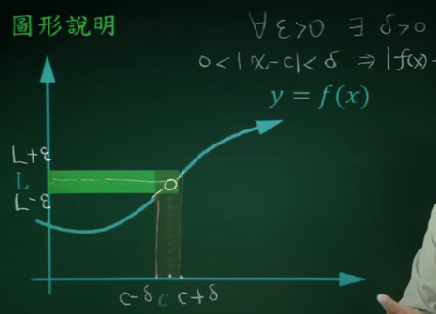
δ表示与点a的距离,ε表示与f(a)的误差

1.将过去的趋近,逼近,靠近这样的动态描述,用ε和δ两个常数来静态的描述。
2.过去是现有x趋于点a,才有x趋于点a,f(x)的界限为L。变成了先有y轴上的误差范围ε,再有x轴上的距离范围δ。所以对于任意的ε,只要可以找到满足条件的δ,这个定义就保证,x趋于点a时函数的极限值存在。
3.在这个定义里面很清楚的规定了,x≠a,x与a相距δ
使用极限的严格定义,证明某函数的x趋于点a的极限为L



补充:函数在某点处极限存在,连续,可导

五、林群院士谈微积分
假传万卷书,真传一案例。高铁瞬时速度,某一时刻计算速度是不行的,因为时间为0,路程也为0,速度为 0比0。必须有很小的一段时间,才有路程,才有路程比时间,尽管速度会发生很小的变化,但变化可以忽略掉。
六、中科大 李柏坚
极限
数列的极限
n取的值越大(与无穷大的距离越小),an的值与的0差距越小。另一种说法是当n趋于0时,an的值趋于0,这种说法使人感觉n是随时间运动的,n随着时间变大,an随着n变大而变小,不如第一种说法,只是静态地取一个值,没有时间和运动的感觉。
函数的极限
自变量取的值与某数的距离越小(但不与该数相等),函数(含变数之数)与极限值的距离越小。
极限的严格定义
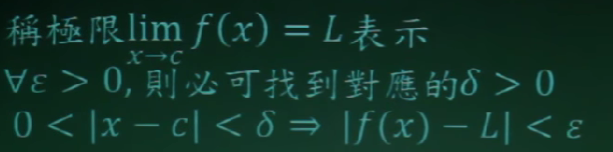
Given epsilon>0,choose δ=…,if 0<|x-c|<δ, => |f(x)-L|
极限的证明
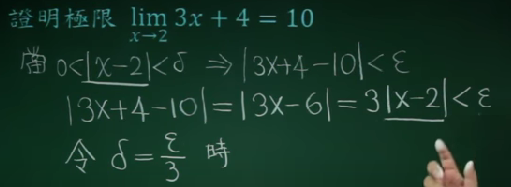
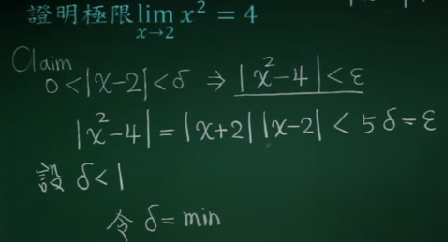
极限的通常求法
中间值定理

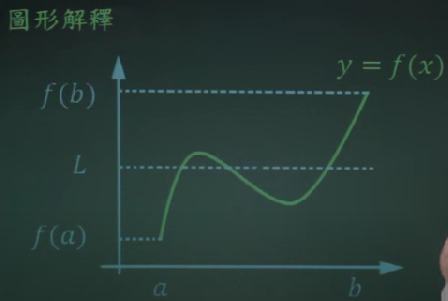
衍生的Bozano定理

也叫勘根定理

连续和可微
连续
若f(x)在点a处连续,则f(a)=lim_{x->a}f(x)
可微
若f(x)在点a处可微,则lim_{x->a}f(x)-f(a)/x-a存在
可微=>连续

连续!=>可微

均值定理
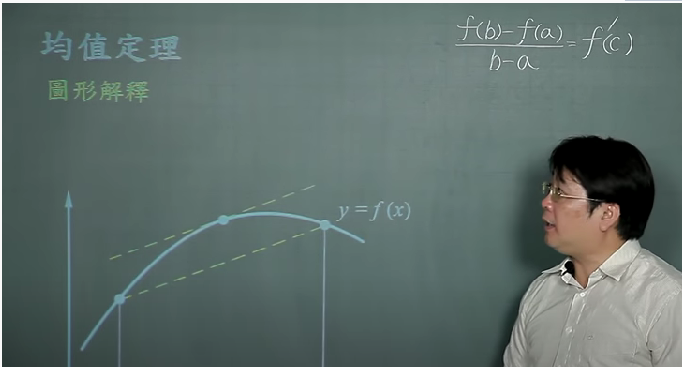
f是一个可微的函数,两点a,b构成的割线的斜率与过其中一点c的切线斜率相等
衍生的洛尔定理

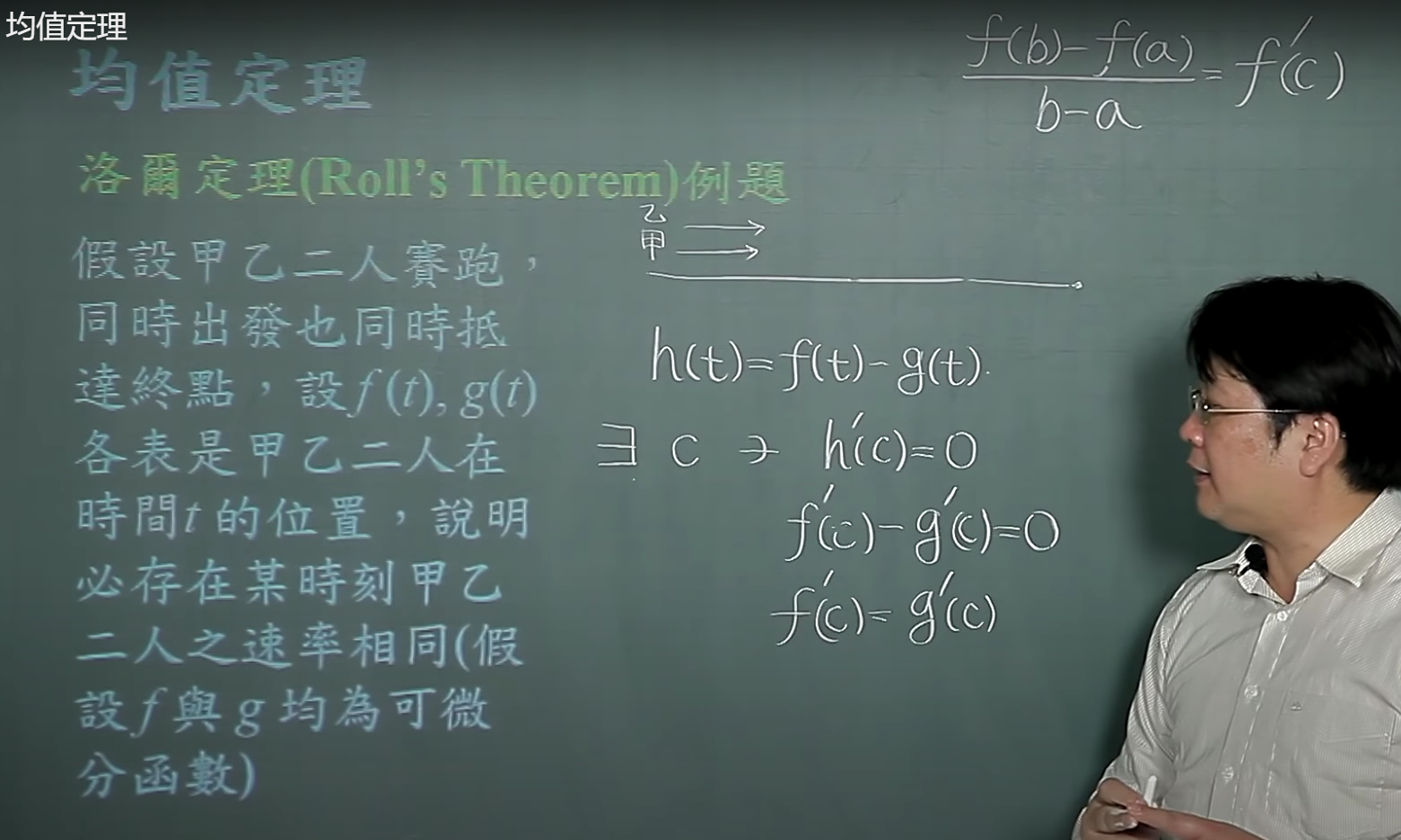
柯西均值定理,使用洛尔定理证明


洛必达法则
右极限的证明





