参考 Youtube——Stepp学院

指数

一开始，指数是正整数连乘的标记

image-20211226084616460

根据面积，可以拓展为正实数的连乘标记

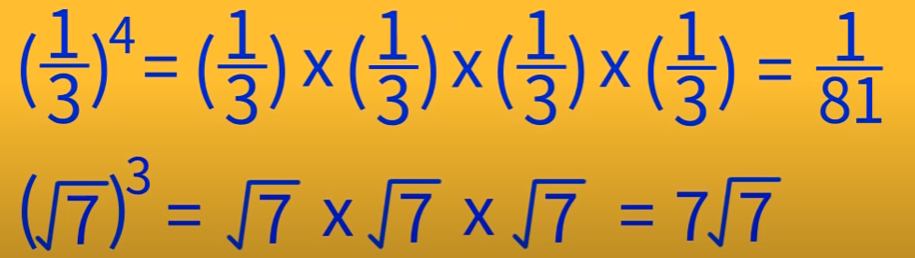
image-20211226084702110

通过在底数的右上角写上指数的记号

三条指数运算规则-指数律

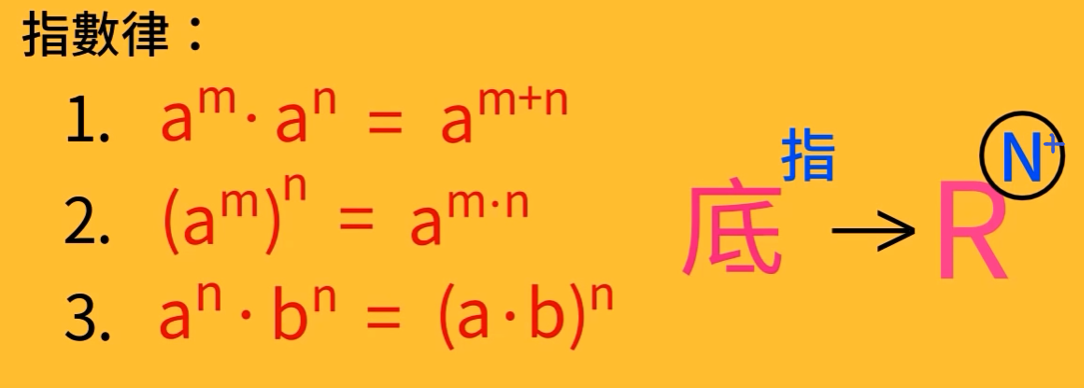
image-20211226085214007

底数为实数，指数为正整数，指数律的证明通过将左边的式子写成连乘的形式，再化为右边的式子。

指数能否为0，负数，分数，不可比数？

从连乘的角度想，会觉得很奇怪。

从形式的角度考虑，从满足指数律的角度，推广指数的范围。

这种推广有两个好处，一个好处是使指数运算具有连续性，另一个好处是对我们的计算和分析具有一定的帮助。

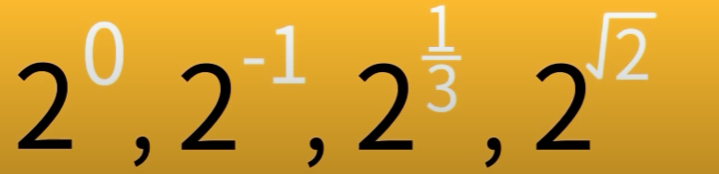
image-20211226085440736

指数的扩充

指数为0

image-20211226090007040

底数为0，a^0 = a^0/a^0 = 0/0 无定义

指数为负整数

image-20211226090502198

底数为0，a^-n = 1/a^n = 1/0 无定义

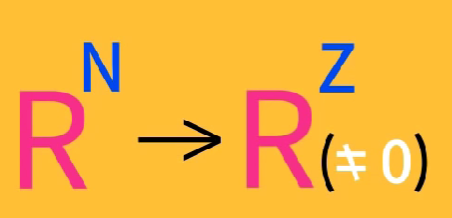
image-20211226090554816

指数为可比数

image-20211226091038741

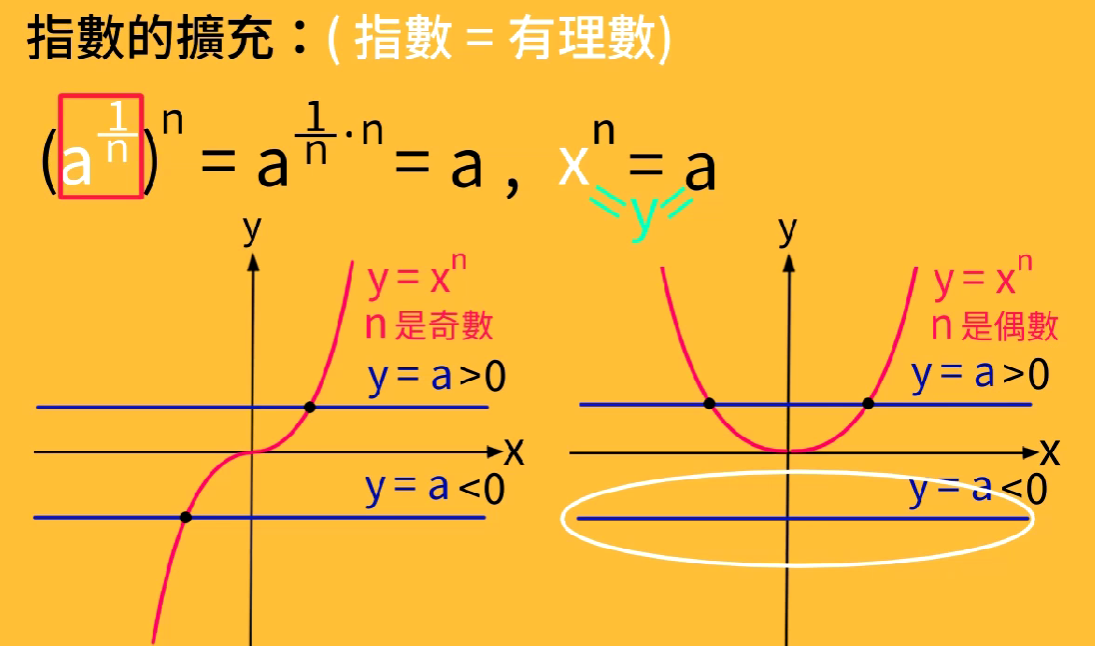
image-20211226091508281

y=x^n 与 y=a 两条曲线的交点情况根据n的奇偶分为两种情况。

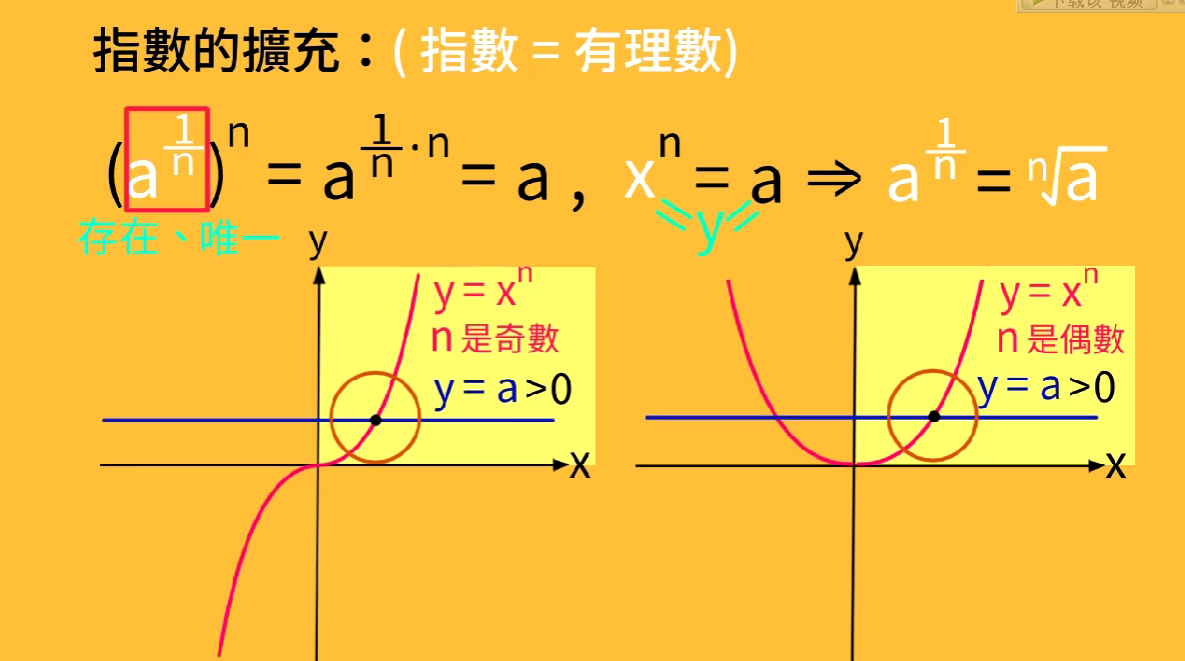
image-20211226091844154

为了使a^1/n的值存在且唯一，我们不再考虑a<0的情况，而且只考虑方程的正根。

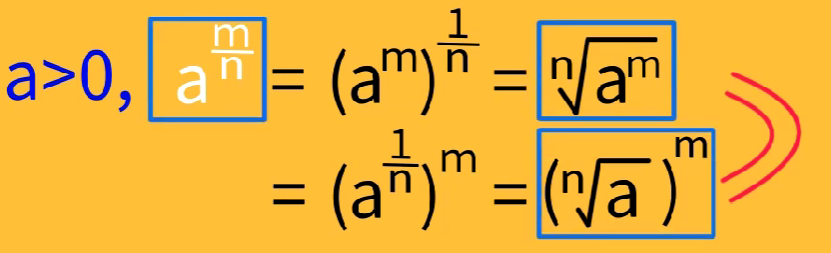
image-20211226091935914

指数为分数，底数＜0时，错误的使用指数律

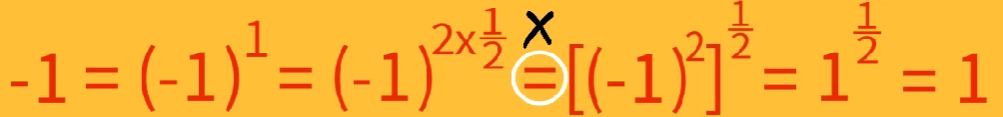
image-20211226092035952

指数为不可比数

image-20211226092549064

对数

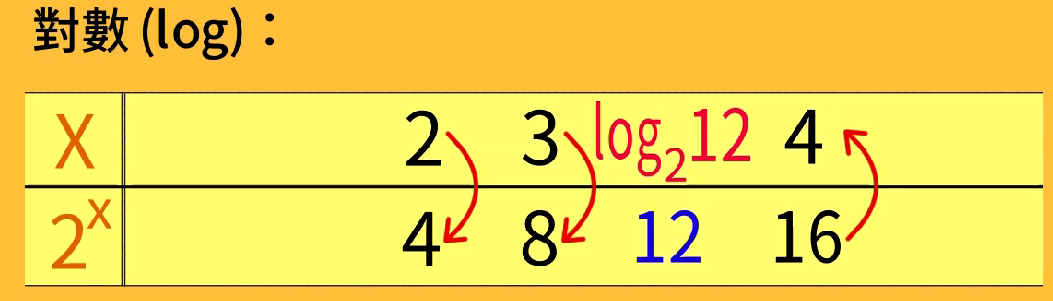
image-20211226093512163

16是2的4次方，12是2的多少次方呢？怎么用一个数表示？

使用符号log，2为底，12为真数，表示使2的次方为12的指数

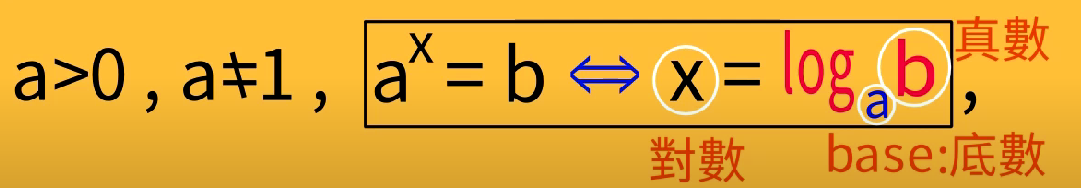
image-20211226093824505

a＞0，因为我们扩展指数的时候就规定了a＞0

为什么a≠1？

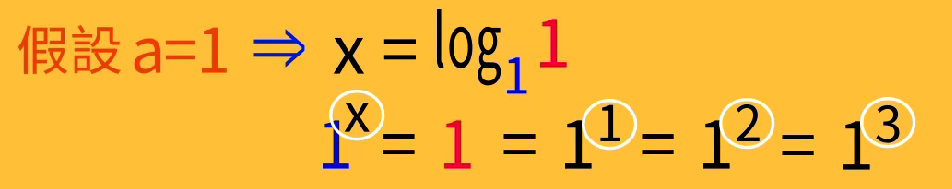
image-20211226094024993

为什么b＞0？因为a>0，a^x>0，只有b＞0，a^x=b才有交点

对数的含义：

image-20211226093908290

对数律

还原公式

从代数的角度看

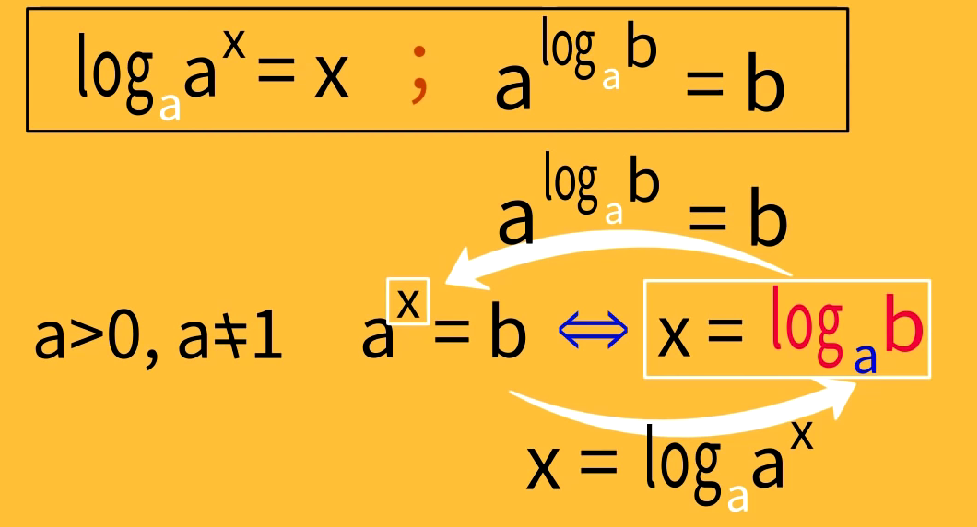
image-20211226094513721

从函数的角度看：指数计算和对数计算互为逆运算

image-20211226094717677

image-20211226094726391

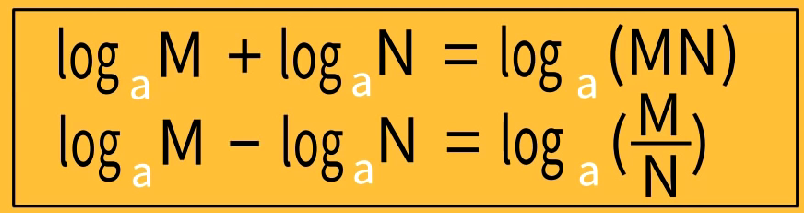
和差公式

image-20211226095257413

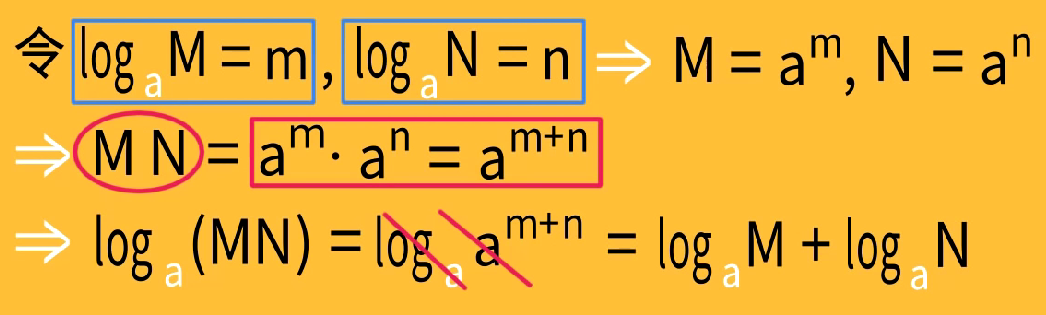
image-20211226095229290

指系数互换公式

image-20211226095642948

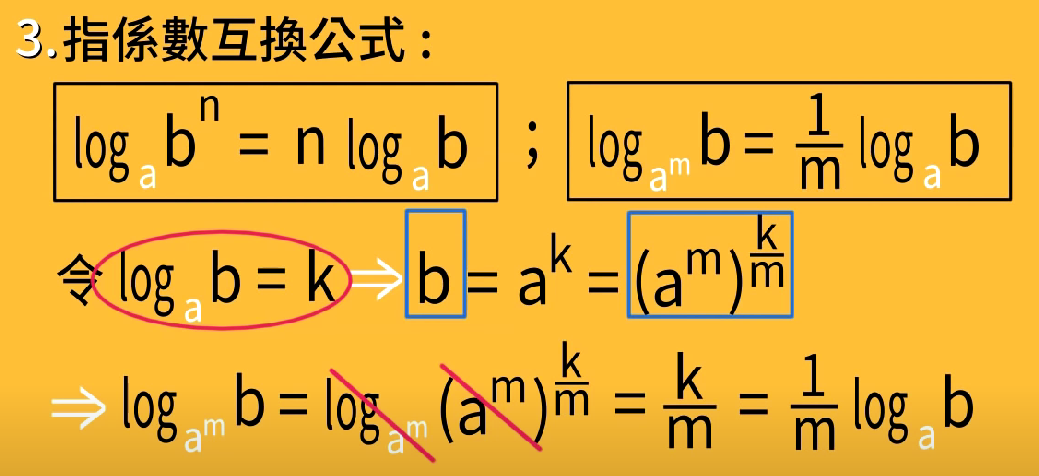
image-20211226095758351

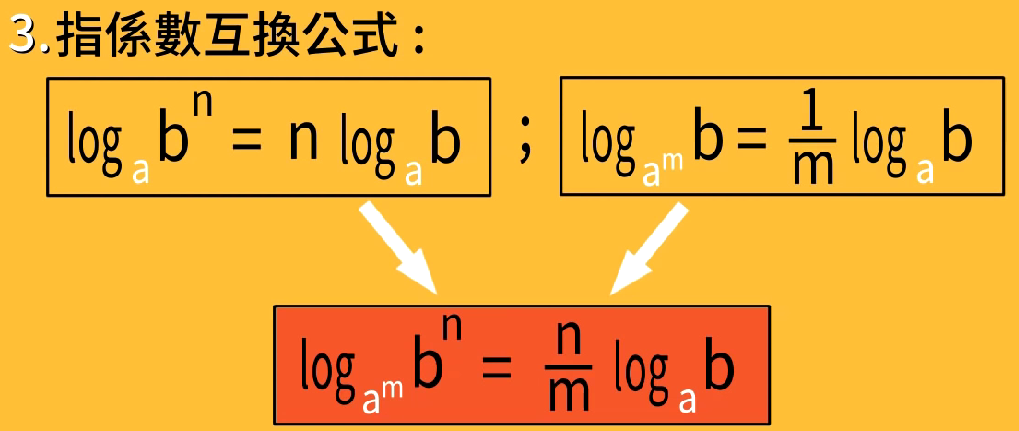
image-20211226095812210

换底公式

image-20211226100051133

image-20211226100219497

倒数公式

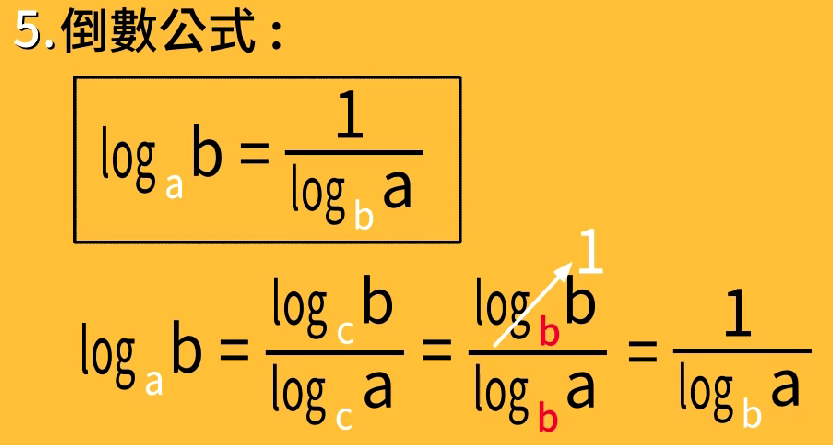
image-20211226100321182

连锁公式

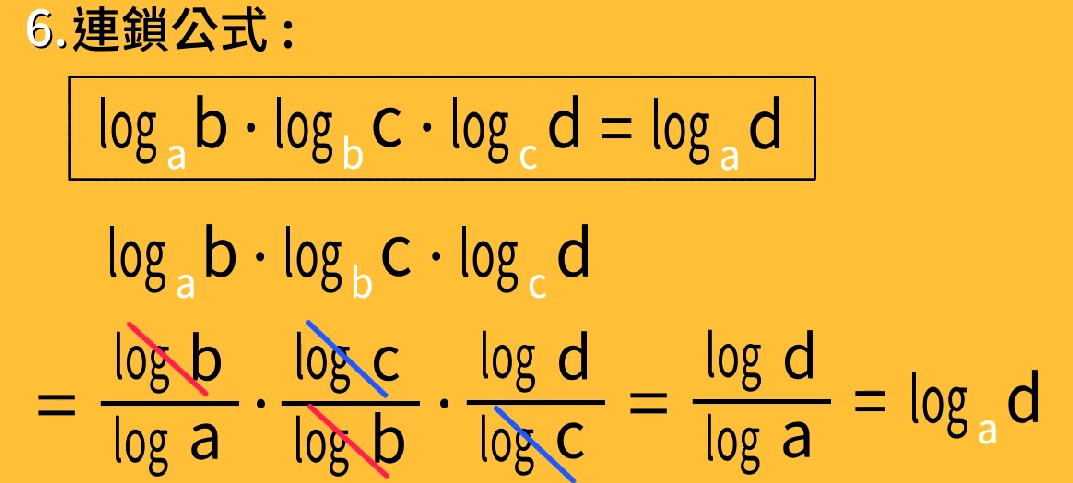
image-20211226100432824

互换公式

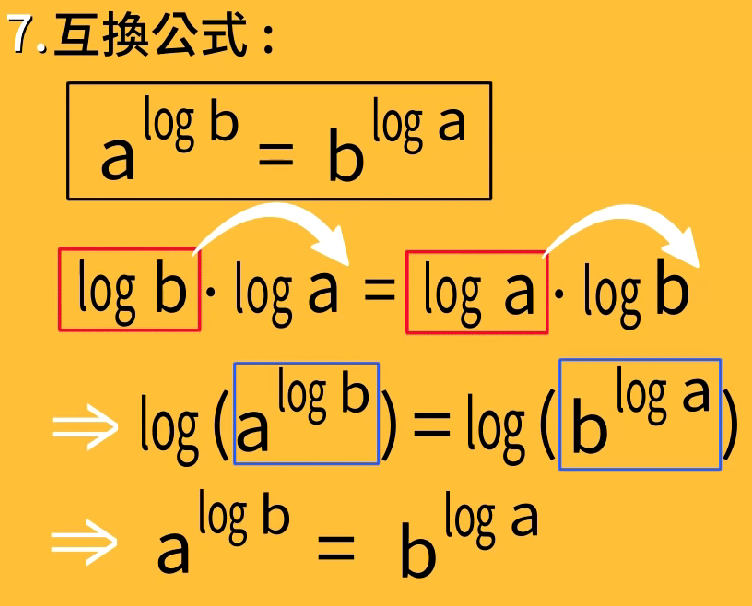
image-20211226100557445