参考中科大-李柏坚的视频

极限

数列的极限

n取的值越大(与无穷大的距离越小)，an的值与的0差距越小。另一种说法是当n趋于0时，an的值趋于0，这种说法使人感觉n是随时间运动的，n随着时间变大，an随着n变大而变小，不如第一种说法，只是静态地取一个值，没有时间和运动的感觉。

函数的极限

自变量取的值与某数的距离越小(但不与该数相等)，函数(含变数之数)与极限值的距离越小。

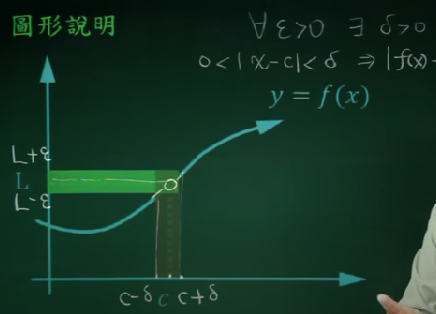
极限的严格定义

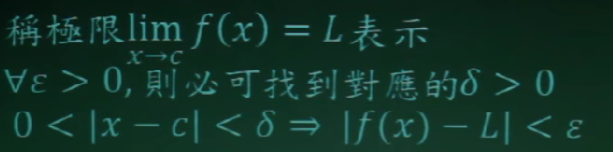
image-20220111191059047

Given epsilon>0，choose δ=…，if 0<|x-c|<δ, => |f(x)-L|c, f(x)->L（x的取值于c的距离越小，f(x)的值与L的距离越小）

image-20220113231902965

极限的证明

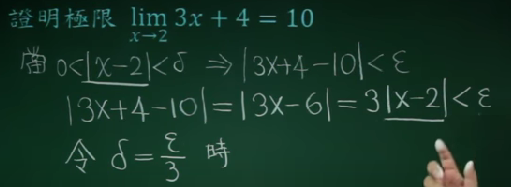
image-20220113231952782

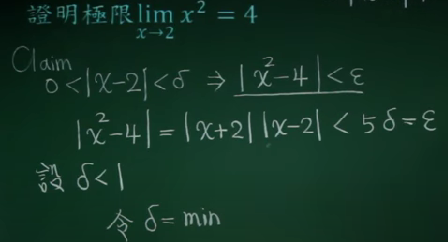
image-20220113232020888

连续和可微

连续

若f(x)在点a处连续，则f(a)=lim_{x->a}f(x)

可微

若f(x)在点a处可微，则lim_{x->a}f(x)-f(a)/x-a存在

可微=>连续

image-20220113211326879

连续!=>可微

image-20220113211715257

均值定理

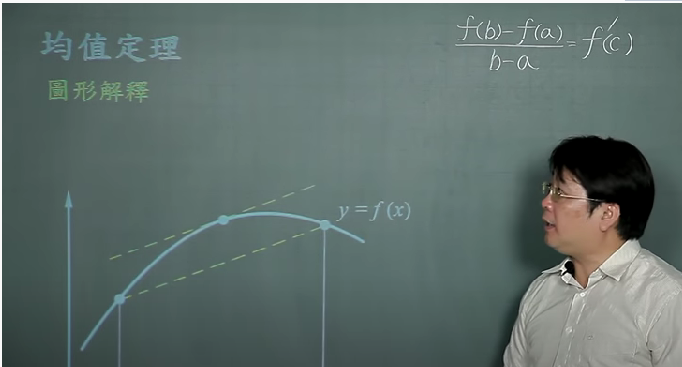
image-20220113220739771

f是一个可微的函数，两点a，b构成的割线的斜率与过其中一点c的切线斜率相等

衍生的洛尔定理

image-20220113221202452

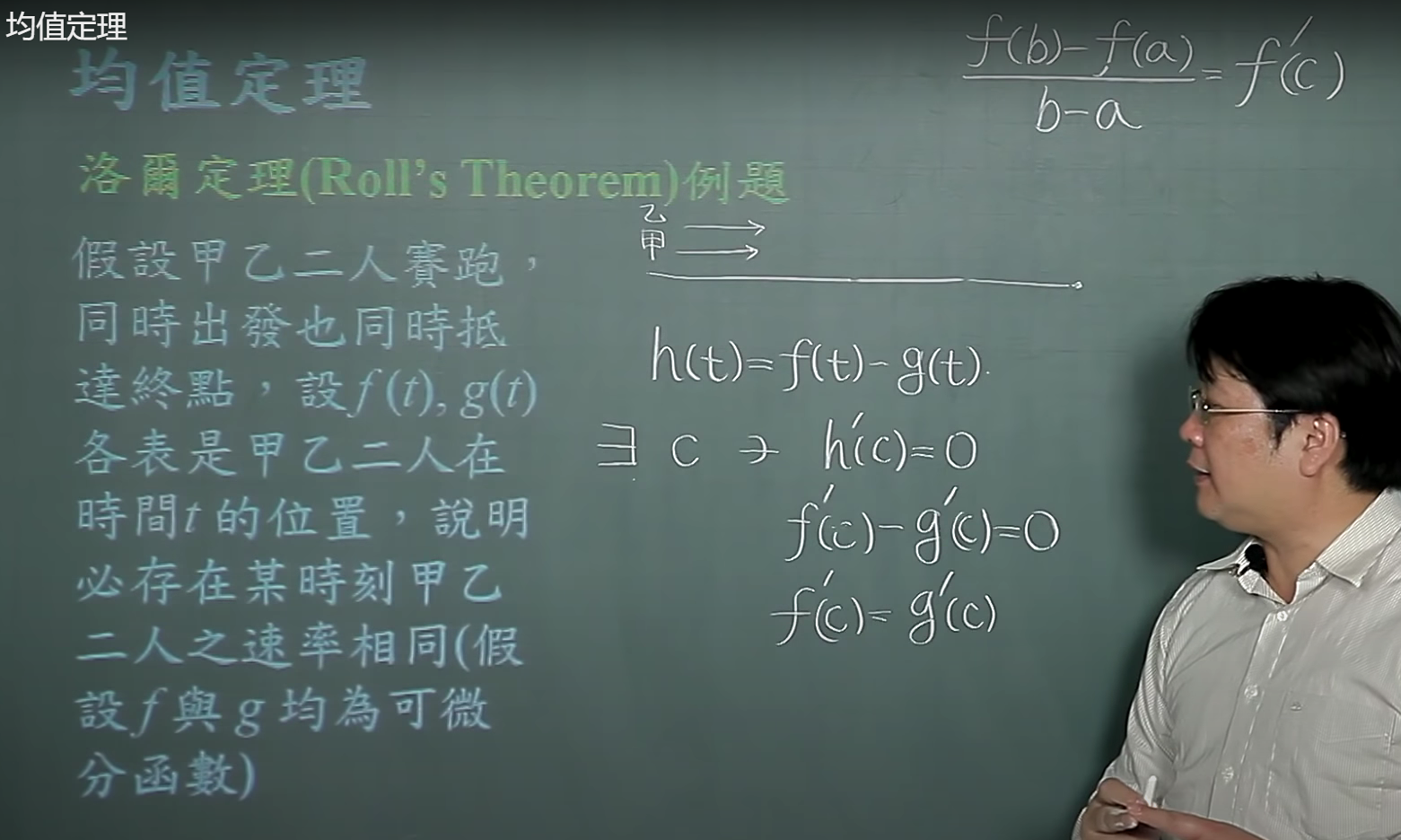
image-20220113223911254

柯西均值定理，使用洛尔定理证明

image-20220113230916610

image-20220113225049046

洛必达法则

右极限的证明

image-20220113230623253

image-20220113231503239

z∈(c,x)，x->c，那么z->c，此时认为z可用x替换

左极限同理。